不相关随机变量(uncorrelated random variables)是一类随机变量,是指相互间没有线性关系的随机变量。如果随机变量ξ,η的相关系数r=0,则称ξ,η不相关。显然,如果ξ,η相互独立,则必定不相关。且下述事实等价:1.ξ,η不相关,即r=0;2.cov(ξ,η)=0;3.Eξη=EξEη;4.D(ξ+η)=Dξ+Dη。 一般地,若ξ,η不相关,它们未必相互独立,但当(ξ,η)是二维正态分布时,独立与不相关等价1。
基本概念不相关随机变量是指两个变量的相关系数为0的变量,是相互间没有线性关系的变量。变量间的关系主要有互不相容、对立、独立和互不相关。
互不相容:若两事件A与B不能同时发生,则称A与B是互不相容事件,或称互斥事件,记作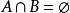 。
。
对立:在互不相容的基础上再加一个条件,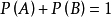 。通俗的说所谓对立事件,有你没我,有我没你,咱俩之间必须有一个。
。通俗的说所谓对立事件,有你没我,有我没你,咱俩之间必须有一个。
独立:设A,B是两事件,如果满足等式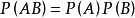 ,则称事件A,B相互独立,简称A,B独立。
,则称事件A,B相互独立,简称A,B独立。
不相关:若随机变量 X 和 Y 的相关系数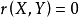 ,称 X 与 Y 不相关,众所周知,独立变量一定不相关(自然要求方差有限),不独立变量也可以不相关,单位圆内的均匀分布即其一例。
,称 X 与 Y 不相关,众所周知,独立变量一定不相关(自然要求方差有限),不独立变量也可以不相关,单位圆内的均匀分布即其一例。
相关关系与相关系数基本介绍相关关系是一种非确定性的关系,相关系数是研究变量之间线性相关程度的量。由于研究对象的不同,相关系数有如下几种定义方式。
简单相关系数:又叫相关系数或线性相关系数,一般用字母r 表示,用来度量两个变量间的线性关系。
定义式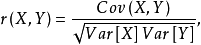
其中,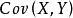 为X与Y的协方差,
为X与Y的协方差,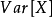 为X的方差,
为X的方差,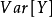 为Y的方差
为Y的方差
复相关系数:又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如,某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。
典型相关系数:是先对原来各组变量进行主成分分析,得到新的线性关系的综合指标,再通过综合指标之间的线性相关系数来研究原各组变量间相关关系2。
相关系数的性质这里,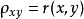 ,
,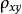 是一个可以表征
是一个可以表征 和
和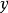 之间线性关系紧密程度的量。它具有两个性质:
之间线性关系紧密程度的量。它具有两个性质:
(1)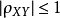
(2)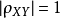 的充要条件是,存在常数a,b,使得
的充要条件是,存在常数a,b,使得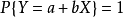
由性质衍生:
a. 相关系数定量地刻画了 X 和 Y的相关程度,即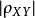 越大,相关程度越大;
越大,相关程度越大;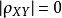 对应相关程度最低;
对应相关程度最低;
b. X 和Y 完全相关的含义是在概率为1的意义下存在线性关系,于是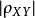 是一个可以表征X 和Y 之间线性关系紧密程度的量。当
是一个可以表征X 和Y 之间线性关系紧密程度的量。当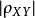 较大时,通常说X 和Y相关程度较好;当
较大时,通常说X 和Y相关程度较好;当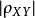 较小时,通常说X 和Y相关程度较差;当X和Y不相关,通常认为X和Y之间不存在线性关系,但并不能排除X和Y之间可能存在其他关系。
较小时,通常说X 和Y相关程度较差;当X和Y不相关,通常认为X和Y之间不存在线性关系,但并不能排除X和Y之间可能存在其他关系。
不相关和独立若X和Y不相关,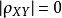 ,通常认为X和Y之间不存在线性关系,但并不能排除X和Y之间可能存在其他关系;若
,通常认为X和Y之间不存在线性关系,但并不能排除X和Y之间可能存在其他关系;若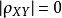 ,则X和Y不相关。
,则X和Y不相关。
若X和Y独立,则必有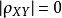 ,因而X和Y不相关;若X和Y不相关,则仅仅是不存在线性关系,可能存在其他关系,如
,因而X和Y不相关;若X和Y不相关,则仅仅是不存在线性关系,可能存在其他关系,如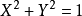 ,X和Y不独立。
,X和Y不独立。
因此,“不相关”是一个比“独立”要弱的概念。
判定方式两个变量是不是相关变量需要用相关系数r来判定,相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度。相关系数r的计算方式如下:
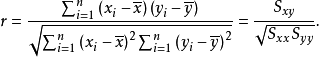 式中:
式中:
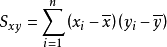 ,称为
,称为 与
与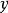 的离均差积和;
的离均差积和;
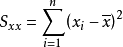 ,称为
,称为 的离均差平方和;
的离均差平方和;
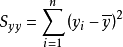 ,称为
,称为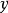 的离均差平方和3。
的离均差平方和3。
计算出的 值可能出现以下几种情况:
值可能出现以下几种情况:
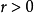 ,正相关;
,正相关;
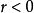 ,负相关;
,负相关;
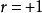 ,完全正相关;
,完全正相关;
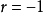 ,完全负相关;
,完全负相关;
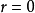 ,无相关。
,无相关。
且:
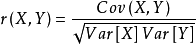 其中
其中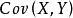 为X与Y的协方差,
为X与Y的协方差,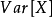 为X的方差,
为X的方差,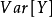 为Y的方差。
为Y的方差。
当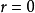 时,称X,Y为不相关变量4。
时,称X,Y为不相关变量4。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国