[科普中国]-无穷维黎卡提微分方程

无穷维黎卡提微分方程(Riccati differential equation for infinite dimensional system)是无穷维线性系统二次最优控制问题中引出的一类算子微分方程。

概念无穷维黎卡提微分方程(Riccati differential equation for infinite dimensional system)是无穷维线性系统二次最优控制问题中引出的一类算子微分方程。由无穷维线性系统二次最优控制问题引入的算子微分方程：

称为无穷维黎卡提微分方程，这里A是C0算子半群的母元，Q*=Q≥0，Q*1=Q1≥0，R*=R≥δI>0，M=BR-1B*，B是线性有界算子，而P*(t)=P(t)是无穷维希尔伯特空间上的对称算子。该黎卡提微分方程的解P(·)，可以视为下述内积黎卡提微分方程：

的解，其中x，y∈D(A)。也可以把P(·)视为黎卡提积分方程：

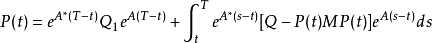的解。

微分算子在数学中，微分算子是定义为微分运算之函数的算子。首先在记号上，将微分考虑为一个抽象运算是有帮助的，它接受一个函数得到另一个函数（以计算机科学中高阶函数的方式）。

最常用的微分算子是取导数自身。这个算子的常用记号包括：d/dx,D，这里关于哪个变量微分是清楚的，以及Dx，这里指明了变量。一阶导数如上所示，但当取更高阶n-次导数时，下列替代性记号是有用的：dn/dxn,Dn,Dxn。1

记号D的发明与使用归于奥利弗·亥维赛，他在研究微分方程中考虑了如下形式的微分算子

另一个最常见的微分算子是拉普拉斯算子，定义为

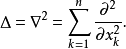另一个微分算子是Θ算子，定义为

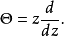有时候这也称为齐次算子，因为它的本征函数是关于z的单项式：

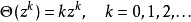在n个变量中齐次算子由

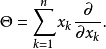给出。与单变量一样，Θ的本征空间是齐次多项式空间。1

最优控制问题最优控制理论所研究的问题可以概括为：对一个受控的动力学系统或运动过程，从一类允许的控制方案中找出一个最优的控制方案，使系统的运动在由某个初始状态转移到指定的目标状态的同时，其性能指标值为最优。这类问题广泛存在于技术领域或社会问题中。

例如，确定一个最优控制方式使空间飞行器由一个轨道转换到另一轨道过程中燃料消耗最少，选择一个温度的调节规律和相应的原料配比使化工反应过程的产量最多，制定一项最合理的人口政策使人口发展过程中老化指数、抚养指数和劳动力指数等为最优等，都是一些典型的最优控制问题。最优控制理论是50年代中期在空间技术的推动下开始形成和发展起来的。苏联学者Л.С.庞特里亚金1958年提出的极大值原理和美国学者R.贝尔曼1956年提出的动态规划，对最优控制理论的形成和发展起了重要的作用。线性系统在二次型性能指标下的最优控制问题则是R.E.卡尔曼在60年代初提出和解决的。

最优控制的实现离不开最优化技术，最优化技术是研究和解决最优化问题的一门学科，它研究和解决如何从一切可能的方案中寻找最优的方案。也就是说，最优化技术是研究和解决如何将最优化问题表示为数学模型以及如何根据数学模型尽快求出其最优解这两大问题。一般而言，用最优化方法解决实际工程问题可分为三步进行：

①根据所提出的最优化问题，建立最优化问题的数学模型，确定变量，列出约束条件和目标函数；

②对所建立的数学模型进行具体分析和研究，选择合适的最优化方法；

③根据最优化方法的算法列出程序框图和编写程序，用计算机求出最优解，并对算法的收敛性、通用性、简便性、计算效率及误差等作出评价。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学