[科普中国]-马氏决策

简介

马氏决策一类可连续进行观察的随机动态系统的最优化决策。根据在各时刻观察到的状态，从允许的决策(控制、措施等)集合中选用一个决策，在这里假定状态和决策两者都不依赖于系统的过去的历史。在各个时刻选取决策的目的，是使系统运动的全过程达到某种最优运行效果的决策规则，称为马氏决策。即每个时刻t选取决策的规则，即与系统在t 以前的历史无关，又是与当前系统状态i所对应的决策ft(i)，i∈S，S是系统全体状态所成的集合。若各个时刻的决策规则都是相同的马氏决策，则称为平稳决策。由于平稳决策的简单性，因此它是实际应用中特别重要的一类决策。马氏决策过程是动态规划与马尔可夫过程结合的产物，由贝尔曼(Bellman，R.)1957年正式提出并借助于最优性原理求解最优决策的方法。后来，有人发现寻求最优决策问题可以化为求解相应的线性规划问题。目前，它已在设备的更换与维修、库存论、排队论、控制工程、可靠性理论、搜索论、水库调度、林渔业管理、通讯网络等的最优化问题中都有应用，并正向工程、生物、经济等领域渗透。

研究者注意的问题主要有：各类模型及其更一般化的研究;状态部分可观察、适应性等模型的理论探讨；特殊模型更有效的解法；如何用易于处理的模型去逼近复杂的模型等问题1。

发展概况50年代R.贝尔曼研究动态规划时和L.S.沙普利研究随机对策时已出现马尔可夫决策过程的基本思想。R.A.霍华德(1960)和D.布莱克韦尔(1962)等人的研究工作奠定了马尔可夫决策过程的理论基础。1965年，布莱克韦尔关于一般状态空间的研究和E.B.丁金关于非时齐（非时间平稳性）的研究，推动了这一理论的发展。1960年以来，马尔可夫决策过程理论得到迅速发展，应用领域不断扩大。凡是以马尔可夫过程作为数学模型的问题，只要能引入决策和效用结构，均可应用这种理论。

马氏决策模型介绍有限马氏决策是指状态集和决策集均有限的马氏决策过程，离散时间有限马氏决策模型由五重组组成：

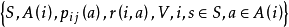
其中各元的含义如下：

（1）状态集S：由系统所有可能的状态组成，表示决策者采取决策的依据，非空。对于有限马尔可夫决策过程来说，S是有限的，用符号i、j、k等来表示状态。

（2）决策集A：表示可供选择的决策范围，对状态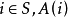 是在状态 i 处可用的决策集，也非空。对于有限马尔可夫决策过程，决策集A(i)是有限的，通常用a来表示决策。

（3）转移概率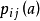 ：表示系统在决策时刻n处于状态i，采取决策 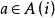时，则系统在n+1时处于状态 j 的概率，它与决策时刻n无关。

（4）报酬函数 r(i，a)：表示系统在决策时刻n处于状态i，采取决策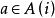 时，系统在本阶段获得的报酬，假定报酬函数 r(i，a)一致有界。

（5）准则函数V：考虑无限阶段的系统期望折扣总报酬准则。即在策略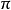 下的无限阶段的期望总报酬为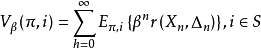： ，其中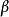 表示折扣因子，如折现率。

（6）定义最优值函数：

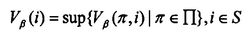
可以证明，最优值函数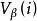 是以下最优方程在可行域B中的惟一解2：

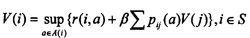
指标衡量策略优劣的常用指标有折扣指标和平均指标。折扣指标是指长期折扣〔把 t 时刻的单位收益折合成0时刻的单位收益的βt(β

采用平均指标的马尔可夫决策过程称为平均模型。业已证明：当状态空间S 和行动集A(i)均为有限集时，对于平均指标存在最优的确定性平稳策略；当S和（或）A(i)不是有限的情况,必须增加条件，才有最优的确定性平稳策略。计算这种策略的算法也已研制出来。

马尔可夫马尔可夫，1856年6月14日生于梁赞，1922年7月20日卒于圣彼得堡。1874年入圣彼得堡大学，受P.L.切比雪夫思想影响很深。1878年毕业，并以《用连分数求微分方程的积分》一文获金质奖章。两年后，取得硕士学位 ，并任圣彼得堡大学副教授。1884年取得物理-数学博士学位，1886 年任该校教授。1896年被选为圣彼得堡科学院院士。1905年被授予功勋教授称号。 马尔可夫是彼得堡数学学派的代表人物。以数论和概率论方面的工作著称。他的主要著作有《概率演算》等。在数论方面，他研究了连分数和二次不定式理论 ，解决了许多难题 。在概率论中，他发展了矩法，扩大了大数律和中心极限定理的应用范围。马尔可夫最重要的工作是在1906～1912年间，提出并研究了一种能用数学分析方法研究自然过程的一般图式——马尔可夫链。同时开创了对一种无后效性的随机过程——马尔可夫过程的研究。马尔可夫经多次观察试验发现，一个系统的状态转换过程中第n次转换获得的状态常决定于前一次（第（n-1）次）试验的结果。

马尔可夫进行深入研究后指出：对于一个系统，由一个状态转至另一个状态的转换过程中，存在着转移概率，并且这种转移概率可以依据其紧接的前一种状态推算出来，与该系统的原始状态和此次转移前的马尔可夫过程无关。马尔可夫链理论与方法已经被广泛应用于自然科学、工程技术和公用事业中。