[科普中国]-正定算子

概念

正定算子(positive definite operator)是相应算子方程可以化为变分问题的一类重要算子。设H是实希尔伯特空间，DA是H的一个线性稠密子集，A是DA→H的线性(不必有界)算子。如果A是对称的，即：

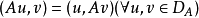
且存在正常数γ，使：

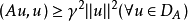
则称A为DA上的正定算子。对DA上的正定算子A，求算子方程Au=f(f∈H)的解u可以化成求泛函：

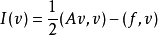
取极小值的极值函数u的变分问题。例如，负拉普拉斯算子A=-Δ是DA={u∈C(Ω)∩C(Ω-)|u=0在∂ Ω上}上的正定算子，其中Ω⊂R是具有C边界∂ Ω的有界区域。狄利克雷问题：

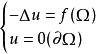
的解就是使泛函：

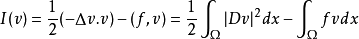
取极小值的极值函数。

算子算子亦称“算符”。逻辑、数学和物理学中对某些变换(映射)或运算的称呼。例如在命题逻辑中，、∨、∧、→、↔等就分别称为否定算子、析取算子、合取算子、蕴涵算子和等值算子；其中是一个一元算子(一元运算)，其余四个都是二元算子(二元运算)。又如在模态逻辑中通常把L(或□)和M(或◇)分别称为必然算子和可能算子，或统称它们为模态算子。

变分问题有关求泛函的极大值和极小值的问题。最早研究的重要变分问题有：

1.最速降线问题：给定不在同一铅垂线上的两点A和B，求出连结A和B的一条曲线使其具有这样的性质：当质点受重力作用沿着这条曲线由A下滑至B时所需时间为最少。

2.短程线问题：求曲面φ(x，y，z)=0上所给二点间长度最短的曲线。这条最短曲线称为短程线或测地线。

3.基本的等周问题：求长为一定的封闭曲线l，使其所围的面积S为极大。2

希尔伯特空间希尔伯特空间是欧几里德空间的直接推广。对希尔伯特空间及作用在希尔伯特空间上的算子的研究是泛函分析的重要组成部分。

设H是一个实的线性空间，如果对H中的任何两个向量x和y，都对应着一个实数，记为(x，y)、满足下列条件：

①对H中的任何两个向量x，y，有(x，y)=(y，x);

②对H中的任何三个向量x、y、z及实数α、β，有(αx+βy，z)=α(x，z)+β(y，z);

③对H中的一切向量x，均有(x，x)≥0，且(x，x)=0的充分必要条件是x=0。则(x，y)称为是H上的一个内积，而H称为内积空间。

如果定义‖x‖=，则在‖0‖下，H构成一个线性赋范空间。3

完备的内积空间称为希尔伯特空间，希尔伯特空间的概念还可以推广到复线性空间上。

欧几里德空间是希尔伯特空间的一个重要特例，希尔伯特空间的另一个最重要的特例是L(G)，设G是n维欧几里德空间中的一个有界闭域， 定义在G上的满足⨜G|f(x)|dx