[科普中国]-等概率假设

概率

在所有可能发生的事件（变量）中，某种事件（变量）发生可能性（或出现相对机会）的大小称为该事件发生的概率。如果在N次（N很大）试验中，某事件X出现了Ni次，则比值Ni/N就叫X事件出现的概率，用

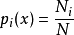表示。例如，我们做抛掷硬币的试验，共抛掷了10000次，其中出现正面的次数接近5000次，则出现正面的概率p正=5000/10000=1/2。由于各种可能发生事件的总数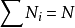，所以

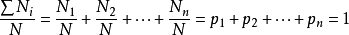即各种可能发生事件的概率之和等于1。这一结论称为概率的归一化条件。

如果表示事件X的量 x 可以连续变化，我们就说 x 具有连续值谱。这时，x 出现在某一间隔 Δx 内的概率Δp(x) 应与这一间隔的位置 x 及大小Δx 有关。变量在 x 附近单位间隔内出现的概率称为概率密度，用 f(x) 表示，于是便有Δp(x)=f(x)Δx。当Δx→0 时，Δp(x) 应写成微分式

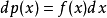概率密度 f(x) 反映了事件概率随 x 而分布的规律，所以又叫概率分布函数。2

等概率假设根据气体动理论，当气体处于平衡态时，虽然其宏观态可以确定，但其微观态却仍不能确定(一切分子都处于永不停息的无规则运动中)，而且也找不到任何理由来说明，某些微观态要比另一些微观态优越。基于这样的事实，1871年，玻耳兹曼提出了著名的等概率假设：当系统处于平衡态时，其各个可能的微观态出现的概率相等。对于气体而言，等概率假设也可以这样来表述：当气体处于平衡态时，其分子向各个方向运动的概率相等。

等概率假设是平衡态统计理论的基础，其正确性虽然不能直接由实验来验证，但由它所得到的许多推论都与客观事实相符，因而便间接地证明了等概率假设是正确的。2

在统计热力学中的表达所有能级分布微观状态数之和构成了系统的总微管状态数，简称总微态数，用 Ω 表示

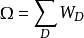
N、U、V确定的粒子系统，可能的能级分布方式D及其微管状态数WD是确定的，系统的总微观状态数Ω也是确定的。也就是说，Ω是N、U、V的函数

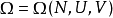因此，可将总微观状态数Ω视为粒子系统的状态函数。

统计热力学假设：对于N、U、V确定的粒子系统，每种微观状态出现的数学概率相等，均等于总微观状态数的倒数

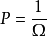该假设称为等概率假设，是统计热力学的基本假设。统计热力学认为在任意短的观测时间（Δtmin→0）内，粒子系统将经历所有可能的微观状态，系统的宏观热力学性质正是所有这些可能微观状态统计平均的结果，而每一种微观状态在统计平均中的贡献是相等的。等概率假设的正确性无法证明，但它显然是合理的，因为我们找不到任何理由相信两种微观状态出现的数学概率会不同。3