[科普中国]-埃尔米特度量

埃尔米特度量(Hermite metric)是殆复流形上的一种度量。设M是殆复流形，具有殆复结构J。若M上黎曼度量g满足g(JX，JY)=g(X，Y)，这里X，Y是M上任意向量场，则g称为M上的埃尔米特度量。

殆复流形殆复流形是其切空间具有复结构的实微分流形。设M是一个微分流形，若它的切丛有复结构，则切丛T(M)上的一个复结构J称为M上的殆复结构。有此结构的流形M称为殆复流形。

微分流形设M是仿紧豪斯道夫 (Hau-sdorff)空间，且是拓扑流形，称A= {(Uα，Фα)|α∈P}是它的地图，如果{Uα|α∈P}是M的开覆盖，Фα是从Uα到n维欧氏空间R的某开集上的同胚。(Uα，Φα)称为坐标卡。如果两个坐标卡 (Uα，Фα)，(Uβ，Φβ) 满足Uα∩Uβ≠Φ，则称Φβ·Фα：Φα(Uα∩Uβ) →Φβ(Uα∩Uβ) 和Φα·Φβ： Φβ(Uα∩Uβ) →Фα(Uα∩Uβ) 为Uα∩Uβ上的坐标变换。如果A的所有坐标变换都是C可微的，则称A为一个C地图，其中1≤r≤∞。r也可等于ω，此时A称为解析地图。拓扑流形M的坐标卡 (U，Φ) 称为与A是Cr相容的，如果任意(Uα，Φα) ∈A，坐标变换Φ·ΦαΦα·Φ均C可微。拓扑流形M的C地图A称为最大的，如果它包含M的所有与之C相容的坐标卡。M上的最大C地图A称为M的C微分结构。(M，A)称为C微分流形，或简称为C流形。当r=∞时，C微分结构也称为光滑结构，C流形也称为光滑流形。r=ω时，C结构也称为解析结构，C流形称为解析流形。C流形(M，A)有时也简记为M。

从直观上看，拓扑流形是局部欧氏空间，局部之间用同胚映射(坐标变换)粘贴在一起。n维C流形，不仅局部同胚于n维欧氏空间，而且局部之间是用C光滑、且其逆也C光滑的坐标变换粘贴在一起。

两个C流形M和N，f：M→N是连续映射，且任一点P∈M，有包含P点的M中的坐标卡(U，Φ)以及包含f(P)的N中的坐标卡(V，)，使得f(U)⊂V，同时，映射°f°Φ-1：Φ(U)→(V)是C光滑的(1≤r≤∞或r=ω)，则称f是C映射。C映射也称为光滑映射，C映射也称为解析映射。其中称为f的局部表示。1

C流形M和N之间的同胚f：M→N，如果f和f均是C映射，则称f是C微分同胚。

度量度量（metric）亦称距离函数，是度量空间中满足特定条件的特殊函数，一般用d表示。度量空间也叫做距离空间，是一类特殊的拓扑空间。弗雷歇（Fréchet，M.R.）将欧几里得空间的距离概念抽象化，于1906年定义了度量空间。

设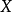为一个非空集合，他的元素叫做点。R是全体实数的集，若函数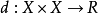对于任意x,y,x∈X合乎条件：

（a）若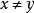，则，并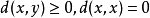；（称作正定性）

（b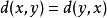）；（称作对称性）

（c）对于一切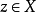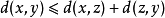，；（称作三角形不等式）

则称函数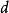为集合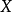上的一个距离函数或度量，d(x,y)为x与y之间的距离。赋予度量d的集合X称为度量空间，记为(X,d)。n维欧几里得空间Rn按通常的度量构成度量空间。区间[0,1]上定义的连续实值函数的集合上赋予由

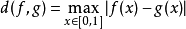确定的度量也是度量空间。在任意非空集合X上定义d(x,x)=0，当x≠y时，d(x,y)=1，则(X,d)也是度量空间。当d满足条件a的后半部分及b、c时，d称为伪度量，赋予伪度量的集合X称为伪度量空间。当d满足条件a、c时，d称为拟度量，赋予拟度量的集合X称为拟度量空间。

在度量空间中，紧性、可数紧性、序列紧性、子集紧性是一致的。可分性、遗传可分性、第二可数性、林德勒夫性是一致的。度量空间必满足第一可数公理，是豪斯多夫空间，完全正规空间，仿紧空间。伪度量空间满足第一可数公理，但一般不是豪斯多夫空间。

埃尔米特法国数学家。生于洛林，卒于巴黎。1842年入巴黎综合工科学校学习。由于先天性右腿残疾，曾遭受到一些人的歧视。但是，不久他就以对椭圆函数诸问题的深入研究，赢得了著名数学家雅可比的赏识。1848年任该校辅导教师。1856年被选为法国科学院院士。1869年成为巴黎综合工科学校和巴黎理学院教授。他还是圣彼得堡科学院的名誉院士。埃尔米特是柯西之后法国杰出的分析学家。他在特殊函数论、数论、高等代数、数学分析等许多方面都做出了很有价值的工作。他研究了椭圆函数和阿贝尔函数的除法和变换，应用椭圆函数解五次方程，解决了相关的力学问题;他推广了高斯研究整系数有限二次型的方法，证明了它们对任意个变量其类数仍是有限的;深入考查了矩阵理论，证明了若矩阵M=M，则其特征根为实数;他还研究了正交多项式中的一类，后来被称为埃尔米特多项式(也称切比雪夫多项式);分析了多项式族与多变数的相似性，研究了整数用代数型表示的问题;引入了复二次型，被称为埃尔米特型。他在1873年证明了数e的超越性，这是一个很著名的结果。他的主要著作收集在4卷本的《埃尔米特著作集》(1905—1917)中。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学