[科普中国]-球体波函数

简介

球体波函数是亥姆霍兹方程的解，通过将方程写在球状坐标中并应用分离变量的技术，就像使用球面坐标导致球谐函数一样。 如果使用扁球状坐标，则称为扁圆球形波函数，如果使用长椭球坐标，则为椭球形波函数。如果不使用亥姆霍兹方程，则采用分离变量的方法，拉普拉斯方程涉及球坐标，球形波函数减少到球面谐波。 具有扁球形坐标，解决方案称为扁平谐波，并且具有长椭球坐标，增长谐波。 两种类型的球形谐波可以用勒让德函数来表示。12

基本方程及推导在球坐标中，标量波动方程为：

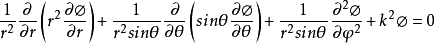
采用分离变量法，令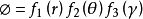，得到

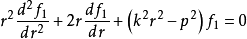
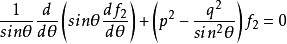
连带勒让德函数的表达式为：

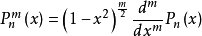
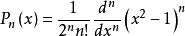
式中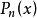，为勒让德函数。与相应的另一独立解为，方程一般解可写为：

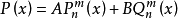
令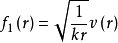，则v(r)满足：

这是一个半奇数的贝塞尔方程，其解为：

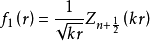
定义球贝塞尔函数为;

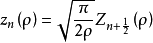
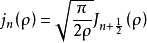
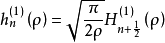
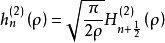
对于球内的散射场，可取基本波函数为：

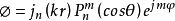
对于球外的散射场，可取基本波函数为：

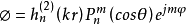
同样，可以由基本波函数的叠加来表示任意波场：

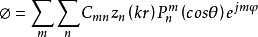
对贝塞尔函数的物理意义与贝塞尔函数的物理意义相似零阶球贝塞尔函数有简单的表达式为：

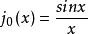
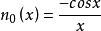
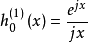
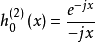
高阶球贝塞尔函数也有显明的初等函数表达式。3