[科普中国]-纯状态反馈

纯状态反馈(pure state feedback)是广义系统的一种反馈形式。它是仅含有系统状态变量的反馈。广义系统亦称奇异系统或描述器系统。一类蜕化的或推广的系统模型。线性系统各状态变量的微分之间不独立的情形，实质上是若干代数式和微分式的耦合。

概念纯状态反馈(pure state feedback)是广义系统的一种反馈形式。它是仅含有系统状态变量的反馈。给定广义系统：1

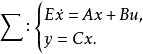形如u=Kx+v(其中K∈R)的反馈称为纯状态反馈，简称状态反馈。在纯状态反馈下闭环系统为：

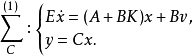闭环系统ΣC(E，A+BK，B，C)具有如下性质：

1.对任意的反馈增益阵K∈Rr×n，闭环系统至多有rank E个有限极点；

2.存在一个K∈R，使得闭环系统具有rank E个有限极点的充分必要条件是广义系统Σ(E，A，B，C)是脉冲能控的；

3.如果Σ(E，A，B，C)是强能控的，则必存在K∈R，使得闭环系统ΣC(E，A+BK，B，C)有rank E个可任意配置的有限极点，即对任给的rank E个共轭成对的复数集合Λ1，总可找到K∈R，使得σ(E，A+BK)=Λ1。

广义系统广义系统亦称奇异系统或描述器系统。一类蜕化的或推广的系统模型。线性系统各状态变量的微分之间不独立的情形，实质上是若干代数式和微分式的耦合。其连续时间情形的数学模型为Ex·=Ax+Bu，Y=Cx，而E为一不满秩的矩阵。这类系统最早于1974年提出，其背景为某些电气网络、经济学中的列昂节夫(Leontief，W.)的投入产出模型、哈罗德(Harrod)和萨缪尔森(Samuelson，P.A.)的国民经济模型，以及若干人口、生态问题等。它也可能是奇异摄动系统中令小参数ε=0时的一级近似。将状态变量x重新组合相当于矩阵E进行相似变换，可以把系统变为m阶(m=rank E)微分方程和n-m个线性代数式的组合。当det(λE-A)不恒为0时，广义系统称为可解的。广义系统除了对应于常规极点的指数运动模式，还具有无穷远极点对应的脉冲模式。它可能包含输入的导数项，从而不满足因果性条件。广义系统的研究成果包括：用矩阵束理论导出的可解性、能控能观性、极点配置、最优控制，以及随机广义系统基于观测与估计的动态反馈等问题。1

反馈原为电子工程物理学和控制论中的概念，指发出的电波信号的回流。在传播学中，指受众对传播者所发出的信息的反应。受众回传给传播者的信息称为反馈信息。传播者通过反馈信息调整、修改、补充下一次传播的内容、方式、渠道、时间和形式，以加强针对性，使传播内容更易为受众所接受，从而收到更好的传播效果。反馈是构成传播过程的要素之一，使传播过程具有双向性质，信息传播与信息反馈相互依存，相互作用。没有信息传播，也就没有信息反馈;受传者对收到的任何形式和种类的信息，都会作出不同形式、不同程度的反应，其中有些能被传播者了解和接受，有些则不能。受众向传播者回传的反馈信息，往往是通过写信、打电话、电报等形式实现的。受传者是反馈信息的信息源。传播者也可主动搜集受众的反馈信息，采取的主要形式是开座谈会、调查、面访等。广播的收听率、电视的收视率、报刊的发行量等，也是受众反馈的一种形式。反馈的特点是：在人际传播中，反馈及时、迅速、直接、明显。大众传播的反馈则与此不同，有如下特点：(一)不及时性：受众不能马上将自己的反应回传给传播者，传播者也不能及时了解受众的反应。在一般情况下，传播者收到反馈信息往往已经过时，难以及时处理反馈信息。(二)间接性：受传者很难直接将自己的反馈信息传达给作者、主持人、编导人员等传播者;传播者则往往要通过第三者——专门机构或组织的调查和统计间接了解受众的反馈。(三)代表性：个别的反馈信息往往不被传播者重视，只有众多的、有代表性的反馈信息才能起到调整下次传播的作用。(四)量化性：反馈往往用数据来体现，如收听率、收视率、发行量等。反馈一般有正反馈和负反馈、前馈和后馈等形式。正反馈指反馈信息与传播者的给定信息基本一致，并对给定信息起一种增强作用。负反馈指反馈信息与传播者的给定信息有某种偏离，并对给定信息起削减作用。受众在传播者发出信息前预先对传播内容和形式提出要求和愿望，称为前馈或预馈;在传播内容抵达受传者后所发出的反馈信息称为后馈。传播者根据前馈调节、修正传播内容和形式，其效果往往是好的，如“听众点歌”、“根据听众要求安排的节目”等。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学