可构造序数(constructive ordinal)是一种特殊的序数。α为可构造序数,是指存在一个记号系统S,使得S中有α的记号。可构造序数都是可数序数,可构造序数的全体构成序数的一个前节,并且可构造序数只有可数多个。从直观上说,可构造序数是可以在自然数上能行表示的序数。事实上,对任何可构造序数,都存在递归相关的单一的记号系统S,使得S中有该序数的记号。此外,可构造序数也恰为递归序数。最早定义可构造序数并对之进行研究的是美国数学家、逻辑学家丘奇(A.Church)。
定义给定如下条件:
(1) 任何一个自然数都不表示两个不同的序数;
(2) 存在如下定义的三个部分递归函数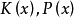 和
和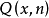 :①对任何表示X的自然数
:①对任何表示X的自然数 ,当X为零、孤立序数或极限序数时,
,当X为零、孤立序数或极限序数时,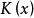 分别取值0 ,1,2;②当X为序数Y的直接后继序数时,对表示
分别取值0 ,1,2;②当X为序数Y的直接后继序数时,对表示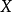 的任何自然数
的任何自然数 而言,
而言,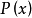 表示Y;③当X为极限序数时,对表示X的任何自然数
表示Y;③当X为极限序数时,对表示X的任何自然数 及每个自然数n而言,
及每个自然数n而言,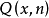 表示
表示 ,而
,而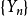 为一个递增的序数序列,使得
为一个递增的序数序列,使得 。
。
满足上述条件(1)与(2)的自然数的集合称为序数的记法系统(system ofnotation for ordinalnumbers),把可用属于一个记法系统的自然数来表示的序数称为可构造序数1。
S3系统在序数的记号系统中,最有用和最方便的是 系统。设为以n为变元的原始递归函数,其定义为:
系统。设为以n为变元的原始递归函数,其定义为: ,用以下的递归定义引入系统
,用以下的递归定义引入系统 基本概念
基本概念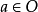 和基本关系
和基本关系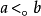 :
:
(1)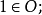
(2) 如果 ,则
,则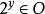 并且
并且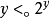 ;
;
(3 )如果自然数序列 具有性质:对每个n,
具有性质:对每个n,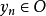 和
和 ,又如果
,又如果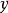 为这样的
为这样的 数,它把
数,它把 作为
作为 的函数而递归地定义,则
的函数而递归地定义,则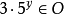 并且对每个n,有
并且对每个n,有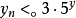 ;
;
(4 )对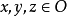 如果
如果 并且
并且 ,则
,则 ;
;
(5) 只有由(1)-(4) 推得时,才有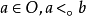
对于 ,以下性质成立(为简单起见,下面把(
,以下性质成立(为简单起见,下面把( 简写成
简写成 ):
):
(1) 如果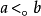 ,则
,则 ;
;
(2) 如果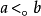 ,则
,则 ;
;
(3) 如果 ,则
,则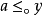 ;
;
(4) 如果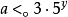 ,则有自然数n,使得
,则有自然数n,使得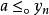 ,这里
,这里
(5)如果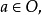 则
则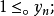
(6) 如果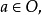 则对任何满足
则对任何满足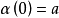 和
和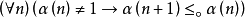 的数论函数
的数论函数 而言,均有k,使得
而言,均有k,使得
(7) 对每个
(8) 如果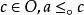 并且
并且 ,则
,则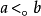 或
或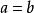 或
或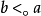 。
。
O中的每个元素a都可以依据下述方法而表示(reprsent)一个序数 对于
对于 有
有 对于
对于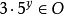 和
和 ,有
,有 设b为O的元素,则当
设b为O的元素,则当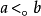 时,便有[a][a]}都是超算术集。
时,便有[a][a]}都是超算术集。
(5) O为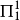 的完备集合,即对任意
的完备集合,即对任意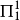 集合E,存在一个原始递归函数φ,使得
集合E,存在一个原始递归函数φ,使得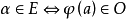 。因此,O不是
。因此,O不是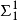 (表示最外边为存在量词的谓词形式的集合) 集合。
(表示最外边为存在量词的谓词形式的集合) 集合。
这里的(3)与(4)是可构造序数理论中重要的有效定理,这两个定理证实了kleene的解析谱系概念的正确性。给定一元(数论) 谓词或给定一个自然数集合N,可以把可构造序数的概念关于N而相对化。令 表示关于N的最小的不可构造序数。记法系统S3的基本概念
表示关于N的最小的不可构造序数。记法系统S3的基本概念 和关系
和关系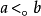 关于N而相对化后分别表示为
关于N而相对化后分别表示为 和
和 ,于是,上面的结果便可以关于N而相对化。例如,(3)的相对化的结果为:存在一个关于N一致的原始递归谓词
,于是,上面的结果便可以关于N而相对化。例如,(3)的相对化的结果为:存在一个关于N一致的原始递归谓词 使得
使得 。如果N为超算术的,则关于N而相对化并非会带来扩充,即
。如果N为超算术的,则关于N而相对化并非会带来扩充,即 是成立的,但是当关于O 而进行相对化时,则可以获得它的真正的扩充
是成立的,但是当关于O 而进行相对化时,则可以获得它的真正的扩充 如果继续进行这种推广,则得到一个(超穷的) 序列
如果继续进行这种推广,则得到一个(超穷的) 序列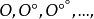 另一方面,可以把可构造序数的概念不限于第二级数类而向更高的任意级数类进行推广。但是,有关这方面的工作,并没有象第二级数类那样获得很多的良好的结果1。
另一方面,可以把可构造序数的概念不限于第二级数类而向更高的任意级数类进行推广。但是,有关这方面的工作,并没有象第二级数类那样获得很多的良好的结果1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国