定义
设有一函数集Δ,再设 对t和x 均不减,如果在集Δ中任取一函数
对t和x 均不减,如果在集Δ中任取一函数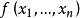 ,恒存在有两数
,恒存在有两数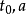 ,使得:
,使得:
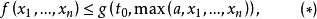 则称
则称 为Δ的控制函数。
为Δ的控制函数。
注意:这里要求 对t和x均不减,如果原耠的
对t和x均不减,如果原耠的 并非不减函数,则可代以
并非不减函数,则可代以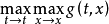 ,因此这个要求一般来说极易满足,既然g为不减函数,显见
,因此这个要求一般来说极易满足,既然g为不减函数,显见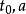 均可换为max(
均可换为max(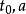 )。
)。
因此,下面永假定所找出的两数是相同的,设记其为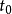 。2
。2
相关性质定理定理1如果函数集Δ含有后继函数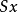 ,且对迭置封闭,则Δ的控制函数,作为t、x的二元函数时,不可能属于Δ。
,且对迭置封闭,则Δ的控制函数,作为t、x的二元函数时,不可能属于Δ。
证明: 如果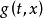 属于Δ,则Sg(t,x)也属于Δ,且应可找出
属于Δ,则Sg(t,x)也属于Δ,且应可找出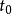 ,使得
,使得
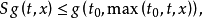 今对t、x均代以
今对t、x均代以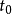 ,将得
,将得
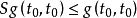 的矛盾结果,定理得证。
的矛盾结果,定理得证。
当Δ为递归生成的函数集时,其控制函数常可利用下法而得到:
如果Δ的开始函数为 ,而对迭置和算子
,而对迭置和算子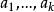 封闭;又,如果能找出一不减函数g(t,x)满足下列条件:
封闭;又,如果能找出一不减函数g(t,x)满足下列条件:
(1)对每一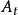 ,均有
,均有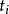 ,使得条件(
,使得条件( )对
)对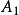 成立;
成立;
(2)如果对于A及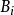 ,均有
,均有 ,使得(
,使得( )对A、对
)对A、对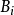 成立,则也有
成立,则也有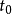 使(
使( )对
)对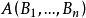 成立;
成立;
(3)在(2)的假设下,也有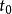 ,使(
,使( )对
)对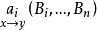 成立,那么,
成立,那么,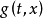 便是该递归生成的函数集
便是该递归生成的函数集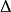 的控制函数。
的控制函数。
如果生成算子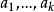 满足一定的条件,则控制函数更易找出。
满足一定的条件,则控制函数更易找出。
定义1如果有一不减函数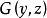 ,使得:
,使得: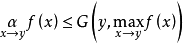 (
(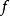 中可合有参数,这时G也含有),则说
中可合有参数,这时G也含有),则说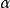 是有界算子,井以
是有界算子,井以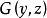 为界,
为界,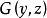 叫做
叫做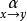 的界(对一般的
的界(对一般的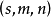 型算子,也有类似的定义,这里不予赘述)。
型算子,也有类似的定义,这里不予赘述)。
今试讨论由有界算子递归生成的函数集。
定义2如果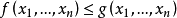 永真,则说
永真,则说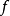 被
被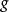 所控制。
所控制。
定理2设函数集Δ是利用迭置及有界算子从某些开始函数而递归生成的,如果Δ的每一个开始函数及它的每一个生成算子的界都被集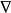 中某一个不减函数所控制,而
中某一个不减函数所控制,而 对迭置封闭,则Δ中每一个函数都被
对迭置封闭,则Δ中每一个函数都被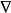 中某一个不减函数所控制。2
中某一个不减函数所控制。2
(文中定理及理论的证明均可参考相应的参考书籍)。
推论如果有不减函数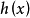 ,使得对一递归生成集的开始函数
,使得对一递归生成集的开始函数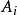 及各生成算子的界
及各生成算子的界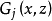 说来,恒有
说来,恒有 ,使得
,使得
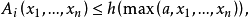
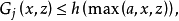 则
则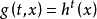 ,即为该递归生成集的控制函数。2
,即为该递归生成集的控制函数。2
注意:这推论是以前对各级初等函数集找控制函数的方法的推广。作为二元函数,控制函数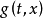 尽管一般不属于原函数集,但对于每个固定的t,g(t,x)却很可能属于原函数集(一般情形也确如此),因此引入:
尽管一般不属于原函数集,但对于每个固定的t,g(t,x)却很可能属于原函数集(一般情形也确如此),因此引入:
定义3如果g(t,x)为函数集Δ的控制函数,且对每个固定的t来说,g(t,x)均属于Δ,则函数列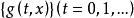 称为Δ的控制骨干。
称为Δ的控制骨干。
定义4设函数集Δ的生成算子为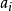 ,如果对函数集中每个函数
,如果对函数集中每个函数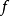 说来,恒可找出一个数
说来,恒可找出一个数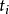 ,使得(
,使得(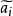 指
指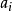 的模算子)
的模算子)
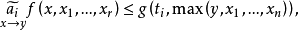 则g(t,x)称为函数集Δ的副控制函数。如果对于每个固定的t,g(t,x)恒属于Δ,则
则g(t,x)称为函数集Δ的副控制函数。如果对于每个固定的t,g(t,x)恒属于Δ,则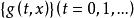 称为
称为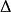 的副控制骨干。
的副控制骨干。
定理3设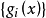 为函数集Δ的副控制骨干,井且Δ为由开始函数经过迭置及若干算子
为函数集Δ的副控制骨干,井且Δ为由开始函数经过迭置及若干算子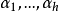 而作成的;今以原开始函数、函数max及
而作成的;今以原开始函数、函数max及 为开始函数,经过迭置及加限算子
为开始函数,经过迭置及加限算子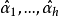 作成的函数集记为
作成的函数集记为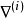 ,则
,则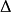 等于诸
等于诸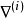 的井集,即
的井集,即
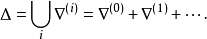
一般说来,加限算子均为初等算子,因此,一般地说,合乎定理3的条件的递归生成集均可分解为初等函数集的并集.
当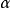 为原始递归式时(这时副控制函数和控制函数同),可以很筒单地作出控制骨干
为原始递归式时(这时副控制函数和控制函数同),可以很筒单地作出控制骨干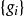 ,而
,而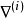 也可很简单地取
也可很简单地取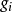 为开始函数(无须兼取
为开始函数(无须兼取 及max为开始函数),其详细内容不做赘述遗,读者可自行探求。2
及max为开始函数),其详细内容不做赘述遗,读者可自行探求。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国