[科普中国]-圆环函数

圆环函数(ring function or toroidal function)是圆环坐标系下求解拉普拉斯方程时出现的一类特殊函数。1拉普拉斯方程是以法国数学家、天文学家P.S.拉普拉斯(Pierre SimonLaplace)命名的偏微分方程。

概念圆环函数(ring function or toroidal function)是圆环坐标系下求解拉普拉斯方程时出现的一类特殊函数，即微分方程：

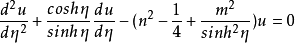的解：

它们是连带勒让德函数Pν(z)和Qν(z)的特殊情形。圆环坐标系(η，θ，φ)和直角坐标系之间的关系是：

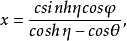
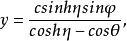
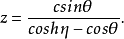
拉普拉斯方程拉普拉斯方程是以法国数学家、天文学家P.S.拉普拉斯(Pierre SimonLaplace)命名的偏微分方程。在电磁学、力学、热学等学科中，拉普拉斯方程用来描述静止场(不随时间变化的场)的特性。令A (x，y，z)是被研究的场量(例如温度)，x、y、z是三维空间直角坐标系的三个坐标量。拉普拉斯方程的具体形式是：2

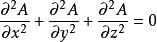采用另一种坐标系，拉普拉斯方程的形式随之改变。为了摆脱坐标系的具体形式，常将拉普拉斯方程写成：

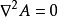静电场中的拉普拉斯方程三维空间的某个区域Ω中充满了同一种各向同性的线性电介质，区域Ω内没有电荷。将Ω中的电位记作V。静电场的规律由拉普拉斯方程▽V=0描述。

恒定磁场中的拉普拉斯方程区域Ω中充满了同一种各向同性的线性磁介质，Ω中没有电流。区域Ω是单连通的。将Ω中的磁标位记作m，恒定磁场的规律由拉普拉斯方程▽m=0描述。

恒定电场中的拉普拉斯方程区域Ω中充满了同一种各向同性的线性导电体，Ω中没有电动势。导电体中的电位V满足拉普拉斯方程▽V=0。

拉普拉斯方程的解拉普拉斯方程的解，决定于区域Ω边界上的场量。边界上给定的场量称边界条件。因此，解静止场的问题，通常是在给定的边界条件下解拉普拉斯方程：①在区域形状简单、边界条件简单的条件下，可以用解析方法解拉普拉斯方程。②用实验方法解拉普拉斯方程，即测量出区域Ω中各处的场量。③利用计算机用数值方法解拉普拉斯方程。随着计算机技术的发展，数值方法得到广泛的应用(见电磁场的数值计算)。

泊松方程若▽A=0的等号右端不是0，而是空间坐标的函数，则此方程称为泊松方程。它是以法国数学家、物理学家S.泊松(S.Poisson)命名的。例如在静电场的情况下，若区域Ω中有电荷体密度ρ时，电位V满足泊松方程：

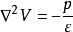其中常数ε为充满Ω的、同一种各向同性线性电介质的电容率。

微分方程微分方程指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。

微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛，可以解决许多与导数有关的问题。物理中许多涉及变力的运动学、动力学问题，如空气的阻力为速度函数的落体运动等问题，很多可以用微分方程求解。此外，微分方程在化学、工程学、经济学和人口统计等领域都有应用。

数学领域对微分方程的研究着重在几个不同的面向，但大多数都是关心微分方程的解。只有少数简单的微分方程可以求得解析解。不过即使没有找到其解析解，仍然可以确认其解的部分性质。在无法求得解析解时，可以利用数值分析的方式，利用电脑来找到其数值解。动力系统理论强调对于微分方程系统的量化分析，而许多数值方法可以计算微分方程的数值解，且有一定的准确度。

含有未知函数的导数，如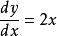的方程是微分方程。 一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程，叫做微分方程。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的叫做偏微分方程。微分方程有时也简称方程。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学