[科普中国]-圆锥函数

概念

圆锥函数(conical function)是在锥形区域中解某些边值问题时出现的一类特殊函数。即微分方程：

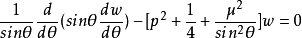
的解：

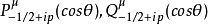
它们是连带勒让德函数Pν(z)和Qν(z)的特殊情形。2

连带勒让德函数连带勒让德函数有两类：第一类连带勒让德函数、第二类连带勒让德函数

连带勒让德函数是连带勒让德方程：

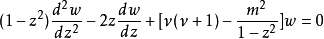
的解，当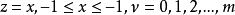为任意整数的情形时，连带勒让德方程为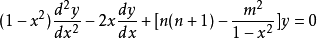的一个解

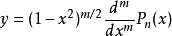
记作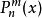.另一个解为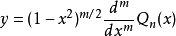

记作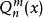，即

.()

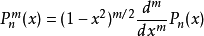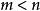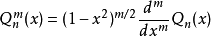
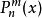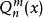，分别称为m阶n次第一类连带勒让德和第二类连带勒让德函数。3

连带勒让德函数的广义傅里叶级数展开连带勒让德函数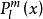在区间[一1，1]上也构成一个正交完备系，可以看作广义傅里叶级数展开的基函数。一个定义在区间[一1，1]上的连续函数，f(x)可展开成以连带勒让德函数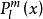为基的广义傅里叶级数

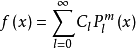
其中广义傅里叶系数为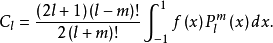

若令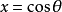,，则以上两式可写成

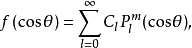
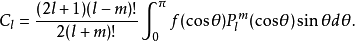
微分方程含有自变量、未知函数和未知函数导数(或微分)的方程称为微分方程。只有一个自变量的微分方程称为常微分方程。一般形式为

F[x，y，y′，…，y(n)]=0

x是自变量，y是x的未知函数y=y(x)，而y′，y″…y(n)依次是函数y对x的一阶、二阶…n阶导数。方程中未知函数的最高阶导数的阶叫做微分方程的阶。如y″+y=0是二阶常微分方程。

有两个或多个自变量的微分方程称为偏微分方程。两个自变量的二阶偏微分方程的一般形式为：F(x，y，u，ux，uy，uxx，uxy，uyy)=0。其中x，y为自变量， u=u(x，y)是x和y的未知函数，ux，uy，uxx，uxy，uyy是u对x，y的一阶和二阶偏导数。

若把某函数及它的导数代入微分方程，能使方程成为恒等式，这个函数就叫该微分方程的解。含n个独立任意常数的n阶方程的解，称方程的通解。一阶和二阶微分方程F(x，y，y′)=0F(x，y，y′y″)=0的通解形式为：y=y(x，c)和y=y(x，c1，c2)。

如果指定通解中的任意一组常数等于某一组固定值，得到微分方程的一个解，叫做特解。

如果函数y及其导数线性地出现在方程中，称为线性微分方程，否则就是非线性微分方程。例如，y″+y=0，uxy=0为线性微分方程，而(y′)=sinx，(1+uy)ux-2uxuyuxy+(1+ux)uxy=0是非线性微分方程。4

边值问题在给定的边界条件下求解偏微分方程组的问 题。在弹性力学中，所要求解的应力分量、应变分量 和位移分量，除应满足平衡微分方程、几何方程以及 广义胡克定律，还必须满足给定的边界条件。若为动力学问题，求出的位移还必须满足初始条件。若 物体为多连通，还需考虑位移单值的条件。按照所 给出的边界条件不同，有三类边值问题。第一类边 值问题：已知作用于物体内的体力及其表面上的面 力，求解这类问题时应满足应力的边界条件。第二 类边值问题：已知作用于物体内的体力及其表面上 的位移，求解时应满足给定的位移边界条件。第三 类问题，又称为混合边值问题：已知作用于物体内的 体力，在一部分表面上面力为已知，而另一部分上位 移是已知的。这三类边值问题可以代表一些简化的 实际工程问题。

边值问题是定解问题之一。只有边界条件的定解问题称为边值问题。二阶偏微分方程(组)一般有三种边值问题：第一边值问题又称狄利克雷问题，它的边界条件是给出未知函数本身在边界上的值；第二边值问题又称诺伊曼边值问题或斜微商问题，它的边界条件是给出未知函数关于区域边界的法向导数或非切向导数；第三边值问题又称鲁宾问题，它的边界条件是给出未知函数及其非切向导数的组合。