完全概率空间 (complete probability space)是一种概率空间。如果概率空间的一切零概率集的子集均属于集,就称为一完全概率空间。1
概念完全概率空间(complete probability space)是一种概率空间。如果概率空间(Ω,F,P)的一切零概率集的子集均属于F,就称(Ω,F,P)为一完全概率空间。对任一概率空间(Ω,F,P),若令F'={A△B:A∈F,B⊂N,N∈F且P(N)=0};P'(A△B)=P(A),A∈F,B⊂N,N∈F且P(N)=0,则(Ω,F',P')为一完全概率空间,称其为概率空间(Ω,F',P)的完全化。
概率空间概率空间是概率论的基础。概率的严格定义基于这个概念。
概率空间(Ω, F, P)是一个总测度为1的测度空间(即P(Ω)=1)。第一项Ω是一个非空集合,有时称作“样本空间”。Ω 的集合元素称作“样本输出”,可写作ω。第二项F是样本空间Ω的幂集的一个非空子集。F的集合元素称为事件Σ。事件Σ是样本空间Ω的子集。集合F必须是一个σ-代数:
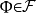
若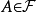 ,则
,则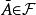 ;
;
若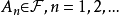 ,则
,则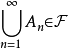
(Ω,F)合起来称为可测空间。事件就是样本输出的集合,在此集合上可定义其概率。
第三项P称为概率,或者概率测度。这是一个从集合F到实数域R的函数,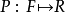 。每个事件都被此函数赋予一个0和1之间的概率值。
。每个事件都被此函数赋予一个0和1之间的概率值。
概率测度经常以黑体表示,例如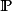 或
或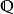 ,也可用符号"Pr"来表示。2
,也可用符号"Pr"来表示。2
概率亦译“或然率”、“几率”。对一个事件的可能性的大小所作的数量方面的估计。在社会和自然界中,某一类事件在相同的条件下可能发生,也可能不发生,这类事件称为“随机事件”。不同的随机事件发生的可能性大小是不相同的,概率就是人们用来表示随机事件发生的可能性大小的一个量。概率的定义有多种:(1)古典定义:一个事件A出现的概率,是A可能出现的情况与全部可能情况的比率。(2)频率定义:一个事件A出现的概率,等于A在若干次试验中出现的频率。
概率是客观存在的统计规律在人们头脑中的反映。作为数学的一门分科的概率论是系统研究概率的科学,而以概率论为工具研究归纳推理的理论就产生了概率逻辑。因此,概率是概率逻辑中的基本概念,与经验的归纳方法不同,它是一种应用数学方法的归纳方法。概率逻辑是作为归纳逻辑的直接继续而产生的。由于归纳逻辑得出的结论,以及假说演绎法的结论,都是或然性的,因而需要从量的方面估计某一结论的或然性,把数学中所制定的精确的概率方法引进逻辑。英国J. S.穆勒的《逻辑体系》一书的归纳部分就已有两章讨论概率。英国数学和逻辑学家布尔也提出了概率的逻辑解释,提出考察关于事件的判断的概率以代替事件本身的概率。1913年苏联数学家和逻辑学家柯尔莫哥洛夫提出了概率的公理化定义,对近几十年概率理论的发展起了积极作用。以后,卡尔纳普在他的归纳逻辑中强调概率的概念应分成两种,即概率1和概率2。概率1是指概率的逻辑概念,概率2是指概率的统计概念。
概率论概率论是研究随机现象数量规律的一门科学,它起源于17世纪法国数学家帕斯卡和费马之间的通信。当一群赌徒请教费马在赌博时谁胜的可能性大时,他开始了现在称之为古典概型的研究。
其后,随着实践及生产的发展,特别是在射击理论、人寿保险、测量误差工作中提出的概率问题,促使人们在概率论的极限理论方面进行了深入的研究。在18和19两个世纪,极限理论成了概率论研究的主题。在大量的工作中以一批苏联学者如车比雪夫、马尔可夫、李雅普诺夫的工作最为出色。马尔可夫使用了所谓截尾术方法,而他师弟李雅普诺夫的特征函数方法则使近200年没有答案的中心极限定理在短短的几页纸上基本得到解决。
由苏联数学家柯尔莫哥洛夫在1929年引进的概率论公理体系,奠定了概率论坚实的数学基础,促进了概率论在理论及应用两方面的发展。柯尔莫哥洛夫的工作标志着近代概率论的诞生。
由于物理学、生物学、医学以及工程技术的推动,概率论的理论课题不断地扩大和深入,应用的领域也日益宽广。目前,概率论在近代物理、无线电与自动控制、工厂产品的质量控制、农业试验、公用事业等方面都找到了重要应用。与此同时,概率论本身的研究则转入以随机过程为中心课题,诸如马氏过程、平稳过程、鞅论等的研究,取得了许多理论上和应用上都有重要价值的结果。近年来,概率论和数学其他分支间的联系也日益加强,用概率论方法不仅可以解决偏微分方程,复变函数论中的一些问题,而且也能证明一些非常著名的结果,如阿提雅-辛格指标定理等。3
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国