“配对”问题
古典概型(等可能概型)中事件概率的计算如下:设在古典概型中,试验E共有N个基本事件.事件A包含了M个基本事件.则事件A的概率为
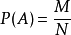
在古典概型中,将A和B搭配在一起算做一个基本事件称为“配对”问题。1
问题举例问题1: 双相异的鞋共
双相异的鞋共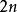 只,随机地分成
只,随机地分成 堆,每堆2只,各堆都自成一双鞋(事件A)的概率是多少?
堆,每堆2只,各堆都自成一双鞋(事件A)的概率是多少?
问题2:从 双相异的鞋
双相异的鞋 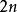 只中随机地选
只中随机地选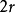 只(
只(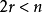 ),没有成对的鞋子(事件A)的概率是多少?
),没有成对的鞋子(事件A)的概率是多少?
问题3:从5双不同的鞋子中任取4只.这4只鞋子中至少有两只配成一双(事件)的概率是多少?
问题4:一个人写了n封信,又在n个信封上分别写了收信人的个人信息(邮编、地址、姓名),然后将信装入信封中,问没有一封信装对(信封上的个人信息与信的内容吻合)(事件A)的概率是多少?
问题5:1,2,…,n中无重复地任选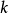 (
(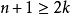 )个数,求正好选出
)个数,求正好选出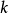 个不相邻数的概率。1
个不相邻数的概率。1
问题解答问题1把2n只鞋分成n堆,每堆2只的分法总数为:
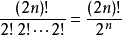 而出现事件A的分法数为
而出现事件A的分法数为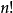 (每双看成一个,n 个分成 n 堆)
(每双看成一个,n 个分成 n 堆)
故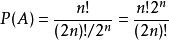 1
1
问题2n双相异的鞋子共 2n 只,随机选取 2r 只 (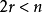 ) ,分法总数为
) ,分法总数为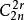 ,即
,即
而出现事件A的分法数为
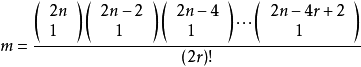 于是
于是 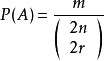 1
1
问题3考虑所选4只鞋的先后次序,总分法为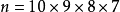 。再来考虑
。再来考虑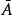 的取法,第一只任取,有10种,第二只有8种,第三、四依此类推,排列数为
的取法,第一只任取,有10种,第二只有8种,第三、四依此类推,排列数为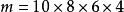 。
。
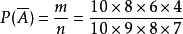 由性质
由性质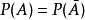 ,得:1
,得:1
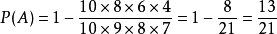
问题4事件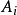 表示 “装对第
表示 “装对第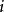 封信:信封上得个人信息与信的内容吻合”,
封信:信封上得个人信息与信的内容吻合”,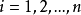 。由性质
。由性质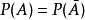 ,得
,得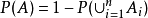 ,这里事件
,这里事件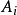 是相容事件组,经计算
是相容事件组,经计算 ,
,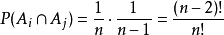 ,
,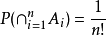 。
。
由公式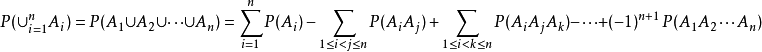
得:
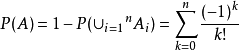 1
1
应用古典概型是一种最简单、最直观的概率模型。
需要注意的是:
①在应用古典概型时必须注意“等可能性”的条件,“等可能性”是一种假设,在实际应用中,我们需要根据实际情况去判断是否可以认为各基本事件或样本点是等可能的;另外,在用排列组合公式计算古典概率时,必须注意不要重复计数,也不要遗漏;
②许多表面上提法不同的问题实质上属于同一类型,比如,箱中摸球、分球入箱、随机取数、分组分配是常见的几种模型,若求其概率均可转化为求“配对”问题的概率。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国