[科普中国]-伯克霍夫遍历定理

概念

伯克霍夫遍历定理(Birkhoff ergodic theorem)是遍历论第一个重要结果。设(X，A，μ，T)是一个保测系统(即T为保测变换)，一个可测函数f：X→R代表对系统的一种测量，{f(x)，f(Tx)，…}给出了轨道{x，Tx，…}的一种信息。在统计力学、信息论中，一个重要问题就是f随时间的平均值的极限：

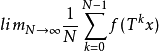是否存在。伯克霍夫(G.D.Birkhoff)针对此问题证明了下述定理，即伯克霍夫遍历定理：设(X，A，μ)为概率空间，T：X→X为保测变换，则有如下结论：1

1.若f∈L1(X)，则：

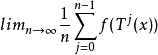μ几乎处处存在。

2.若f∈L(X)，1≤p≤+∞，则：

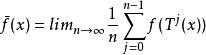亦属于Lp(X)且：

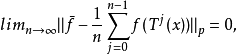
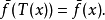
3.对任意f∈Lp(X)，有：

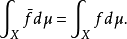
遍历论遍历理论是研究保测变换的渐近性态的数学分支。它起源于为统计力学提供基础的"遍历假设"研究，并与动力系统理论、概率论、信息论、泛函分析、数论等数学分支有着密切的联系。

系统的一个状态在相空间中有一个代表点P=(p,q），系统的运动就对应于点 P在相空间中的运动。如果系统是保守的，其总能量E便是常数，点P的运动就被限制在相空间中的等能面（称为能量面）H=E之上。

假如系统的自由度n非常大,例如在一定容器中气体分子的运动（宏观上微小的体积中仍含有大量的分子），如果与外界没有能量交换，就是一个保守的力学系统。这时 n=3N，N是分子的数目。因为人们无法去解如此巨大数目的哈密顿方程组，也无法实际地测得解方程时所必需的初始资料，所以不可能再用纯经典力学的方法来研究这样的系统。其实，系统中大量分子运动的综合作用才决定出系统的宏观性质。例如，气体的单个分子只是断续地冲撞容器壁，而大量分子冲撞的综合平均作用才形成了气体对器壁的稳定的压强。

为了研究这类本质上是统计性质的运动规律，人们设想同时考虑都是含有N个粒子，处于同一外部条件之中并且具有同一哈密顿量，但微观状态不一样的一切可能的系统。这些系统在相空间中的代表点就不一样。这些宏观条件一样的一切可能的微观系统的全体称为系综(ensemble）。

L.E.玻耳兹曼，特别是J.W.吉布斯建立了完整的统计系综方法，类比于流体力学中的刘维尔定理，证明了系综的概率分布守恒定理。如果用φt(P）表示相点P 经过时间t之后在相空间中达到的点，那么φt便是相空间的一个变换。所谓概率守恒，就是说φt能使一定的概率测度保持不变。

如果某系综相应的概率分布不显含时间，就称做稳定系综。统计力学基本假设之一是认为真实的平衡物理系统在某时刻的状态与其相应的稳定系综在相空间中的点有相同的概率。

可测函数可测函数是分析学中讨论得最广的函数类。它有许多等价的定义方式，这里采用如下定义：设(Ω，F)为可测空间，f(x)是定义在Ω上的实值(或扩充实值)函数。若对任意实数c，恒有{x|f(x)>c}∈F，则f(x)称为(Ω，F)中的可测函数或Ω上的F可测函数。在这个定义中，条件f(x)>c可用f(x)≥c，f(x)