[科普中国]-样本协方差矩阵

定义

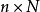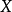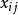通常，我们将 数据矩阵记为 或 ，第i行第j列对应的元素可表示为 ，我们将矩阵表示为 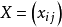。 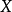的行可以表示为2

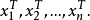或者

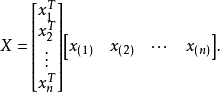其中

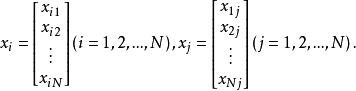第i个变量的样本均值是

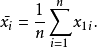
样本协方差矩阵一般形式第i个变量的样本方差是2

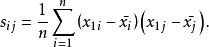
第i个变量和j个变量之间的样本协方差为

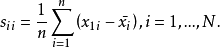
向量 的均值为

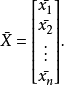称为样本均值向量，或简称为“均值向量”。N×N矩阵

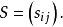称为样本协方差矩阵，或简称为“协方差矩阵”。使用矩阵符号来表示统计量更为简便。

标准形式记

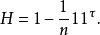
其中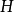， 称为中心矩阵，我们得到如下标准形式

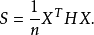
这是样本协方差矩阵的一种简便矩阵表达式。我们总计需要nN个样本点来估计样本协方差矩阵S。转向表格，我们可以将nN个样本点的信息“归纳”到单一矩阵S中。在频谱感知中，我们会得到某些随机变量的长记录数据或大数据维度的一个随机向量。2

应用在多元分析中，样本协方差矩阵的研究是基础。拥有现代数据，矩阵往往非常大，变量数目与样本量相当(即所谓的“大数据”)。在这种环境中，最大特征值或主成分方差的分布往往鲜为人知。在数学物理和概率域，随机矩阵理论的一·个惊喜是：对于相对较小的n和p来说．这些结果似乎能够提供与主成分有关的有用信息。2

假定X是一个p×n数据矩阵。人们通常考虑p维列向量(其协方差矩阵为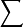 )的n个观测值或情形 。为明确起见，我们假定行 服从独立高斯分布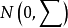 。特别是，平均值已被减去：如果我们也不用担心被n除，则我们将 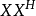称为样本协方差矩阵。在高斯假设下，我们称 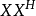“符合Wishart分布。如果=1，则属于“空”情形，我们称其为白色Wishart，类似于时间序列设置，在该设置中，白色频谱在所有频率处具有相同的方差。

多元分析中的大样本工作历来假定n/p(每个变量对应的观测值数)取值较大。如今，p取大值甚至巨值都是常见的，因而n/p取值范围为从中到小。在极端情况下，甚至小于1。

特征值和特征向量分解样本协方差矩阵的特征值和特征向量分解过程可表示为

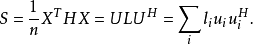
该矩阵包含对角矩阵L中的特征值和作为矩阵u列采集的正交特征向量。

一个基本的现象是，相同的特征值z；要比特征值A。应用范围更广。在空的情形中，当所有总体特征值相同时，这一效果最为明显。2