概念
瑞利商迭代法(Rayleigh quotientiterationmethod)是一种用瑞利商作位移的反幂法。反幂法的收敛性和幂法本身一样是线性的。不像幂法之处是只要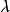 充分接近
充分接近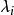 ,反幂法的收敛性系数
,反幂法的收敛性系数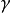 可以任意小。对这一点的观察导致在
可以任意小。对这一点的观察导致在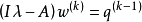 中当
中当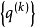 收敛到一特征向量时,每步迭代均选取特征值的“最佳猜测”,自适应地改变参数
收敛到一特征向量时,每步迭代均选取特征值的“最佳猜测”,自适应地改变参数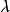 的概念。这样,瑞利商迭代法与反幂法不同之处,在于每一迭代步
的概念。这样,瑞利商迭代法与反幂法不同之处,在于每一迭代步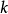 ,在
,在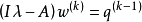 中用瑞利商
中用瑞利商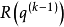 代替
代替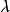 。我们用规范化的
。我们用规范化的 的残量的
的残量的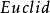 长度来度量向量
长度来度量向量 满足特征向量条件的偏差。具体地说,准则是
满足特征向量条件的偏差。具体地说,准则是
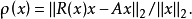 瑞利商迭代法值得注意的是,按我们现在形式上叙述的误差,收敛性是平方的,甚至是立方的(三阶的)。1
瑞利商迭代法值得注意的是,按我们现在形式上叙述的误差,收敛性是平方的,甚至是立方的(三阶的)。1
基本原理定理:设 是按瑞利商迭代法构成的,并假定在每步迭代,对某确定的
是按瑞利商迭代法构成的,并假定在每步迭代,对某确定的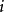 ,
,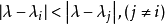 满足,若以
满足,若以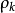 表示残量的
表示残量的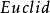 长度,即
长度,即
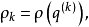 则对于某常数
则对于某常数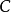 和
和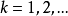 ,
,
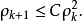
证明:设 表示一个特征向量的估计值,假定
表示一个特征向量的估计值,假定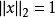 ,且实部
,且实部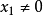 ,这里
,这里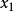 是
是 的第一个分量,设
的第一个分量,设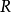 是
是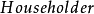 变换使
变换使
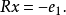 可分解
可分解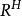 为
为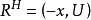 ,类似于下面的分块结论是正确的:
,类似于下面的分块结论是正确的:
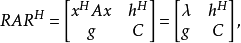 式中显然
式中显然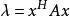 是
是 对
对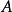 的瑞利商,且
的瑞利商,且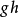 是
是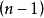 维向量。
维向量。
利用酋阵的性质,得到若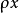 按
按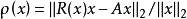 的定义则
的定义则
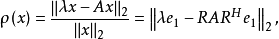 鉴于
鉴于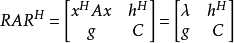 ,得到误差的关系式
,得到误差的关系式
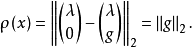
设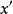 是由瑞利商迭代决定的,它是向量
是由瑞利商迭代决定的,它是向量 的非规范化的后继向量,即设
的非规范化的后继向量,即设
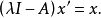 再利用酋阵的性质,求得
再利用酋阵的性质,求得
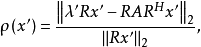 式中
式中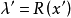 ,以
,以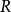 左乘
左乘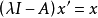 得到
得到
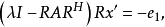 与
与 比较,得到结论
比较,得到结论





 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国