[科普中国]-递归关系

定义

设p0，p1，…，pn，…是一个序列。如果pn和序列中在它前面的若干项联系起来的一个关系式对所有大于等于某个整数n0的整数n都是有效的，则称这个关系式为递归关系(recursive relation)式。

如：设(a0，a1，...，ar，...)是一个序列，把该序列中的ar和它前面的几个ai(0≤io)，n=k--1时成立，则n=k时，

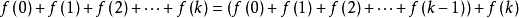
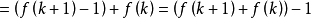
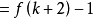
由数学归纳法原理，得到证明。

现在需要做的事情是找出一个显式表示斐波那契数。考虑斐波那契的对于n=2，3，4，…递归关系，并略去f(0)和f(1)值。解决这个递归关系的一种方法是寻找形式为f(n)=qn的一个解。它的第一项是q0=1。发现：f(n)=qn满足斐波那契递归关系当且仅当qn=qn-1+qn-2，或对于n=2，3，4，…有qn-2(q2-q-1)=0。因为假设q≠0，所以得到f(n)=qn是斐波那契递归关系的一个解当且仅当q2-q-1=0，或等价地讲，当且仅当q是二次方程x2-x-1=0的一个根。该方程的根是

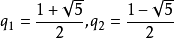于是

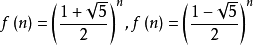是斐波那契递归函数的两个解。由于这个递归关系式线性的（没有f的不是1的方幂）齐次的（没有常数项），所以导出

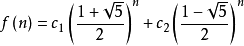对于任意的常数c1和c2，是递归函数的解。

因为斐波那契序列有初始值f(0)=f(1)=1，所以可以通过二元一次方程组来确定常数c1和c2。

n=0时，得：c1+c2=1

n=1时，得：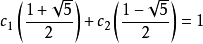

解得：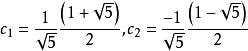

概括起来，有以下定理

**1.**斐波那契数满足公式

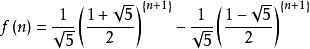对n=0,1,2，...

对于不同的处置，c1和c2将得到不同的值，f(n)的形式也有所不同。

**2.**沿着杨辉三角或Pascal三角形的对角线，从左向上的二项式系数之和等于斐波那契数。更确切地说，对于n≥0，第n斐波那契数f(n)满足

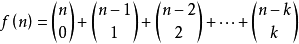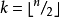其中 .2

河内塔递归关系的另外一个很重要的模型是河内(Hanoi)塔。如下图所示，1，2和3是三根直立的杆子．不妨设，开始时有n个圆盘依大小，自下而上套在杆1上，并且n个圆盘的半径两两不同。现在按照三条规则，将杆1上的圆盘以原样全部转移到杆2或杆3上。这三条规则是：(1)每次只转移一个圆盘；(2)整个转移过程始终保持较小的在较大的上面的形式；(3)有而且仅有三根立杆1，2和3供使用。

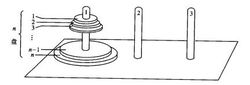
问：最少要移动多少次，才能将杆1上的n个圆盘以原样全部转移到杆2或杆3上?

稍加分析不难看出，按照上述三条转移规则，n个圆盘的转移只能按下面的过程进行：第一步将杆1最上面的n-1个圆盘，借助杆2或杆3转移到其中的一根上，不妨设转移到杆2上。第二步将杆1的最下面的大圆盘转移到杆3上．第三步借助杆1和杆3，再把杆2上的n-1个圆盘转移到那个套有最大圆盘的立杆3上，如下图所示。

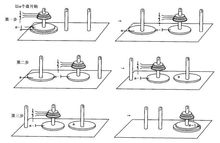
假设hn表示转移n个圆盘所需要的最少移动次数，那么执行第一步需要hn-1次，执行第二步需要一次，执行第三步需要hn-1次，于是最少移动的总次数等于

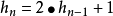
并且初始条件h1=1。显然，hn的表达式也是一个递归关系式。2

应用在平面上有n条直线，假定没有两条直线是平行的，且没有三条直线是共点的，问这个平面被这n条直线分隔成多少个区域?3

**解：**令an表示n条直线将平面分割成的区域数。显然a0=1，当n=1，2，3时，由下图可得，a1=2，a2=4，a3=7。

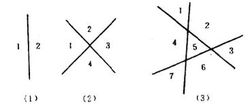
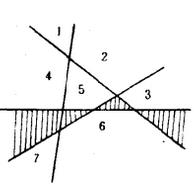
现在假定平面上已有n-1条直线把平面分割成an-1个区域，再在平面上插入第n条直线。它与原n-1条直线相交，得到n-1个不同的交点，这n-1个点把第n条直线分成n段，从而产生了n个新区域。例如在上图的(3)中平面省上三条直线将平面分割成7个区域，现加进第4条直线，与原三条直线相交，得3个交点，产生了4个新区域，如下图阴影部分。因此，我们推知有如下的递归关系：

而a0=1.3