[科普中国]-席夫定理

席夫定理是对开集条件的一种刻画，即在开集条件下，自相似集的测度与维数都有完整的结果。

简介席夫定理是对开集条件的一种刻画，即在开集条件下，自相似集的测度与维数都有完整的结果。

该定理表述为：设E是压缩系数为ci的相似压缩族Si(1≤i≤m)的自相似集，s为其相似维数，则下述条件等价：

1、开集条件成立；

2、ℋs(E)>0。1

开集条件开集条件是加在压缩映射族上的一种条件。

设S1,S2,...,Sm是Rd上的压缩映射，如果存在开集V⊂R使得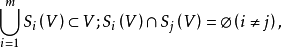则称压缩族S1,S2,...,Sm满足开集条件，亦称该压缩族的不变集E满足开集条件。

自相似集自相似集是一类具有自相似性的分形集合，是最重要的分形集类。

设Φ={φ1,φ2,...,φm}为有限压缩族，所有的φj均为相似压缩，则F称为自相似集。它由具有各向同性的线性压缩族，即相似压缩族生成，其最重要的特征是它的局部与整体具有严格的相似。

自相似集在分形几何的研究中具有非常特殊的地位。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所