[科普中国]-开集条件

开集条件是加在压缩映射族上的一种条件。由席夫(Schief,A.)提出的定理刻画了开集条件，但并没有减少判别开集条件是否成立的难度。

简介开集条件是加在压缩映射族上的一种条件。

设S1,S2,...,Sm是Rd上的压缩映射，如果存在开集V⊂Rd使得则称压缩族S1,S2,...,Sm满足开集条件，亦称该压缩族的不变集E满足开集条件。1

发展开集条件容许相似压缩族作用在某些集合上可以有重叠，但要求重叠不能太多。

由席夫(Schief,A.)提出的定理刻画了开集条件，但并没有减少判别开集条件是否成立的难度。

压缩映射压缩映射亦称巴拿赫压缩映射，是指在度量意义下压缩的映射。

设(X,dX)与(Y,dY)是度量空间，f:X→Y是映射。若存在常数k∈[0,1)，使得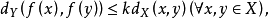则称f为压缩映射，k称为压缩系数。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所