[科普中国]-弗罗斯特曼引理

弗罗斯特曼引理是联系势论与分形几何的一个非常重要的结果，弗罗斯特曼引理与质量分布原理一起通称为弗罗斯特曼引理。

简介弗罗斯特曼引理是联系势论与分形几何的一个非常重要的结果。

设E为Rd中紧集。若ℋα(E)>0，则存在由E支撑的α阶赫尔德正有界波莱尔测度。

质量分布原理质量分布原理是估计豪斯多夫维数的一种常用的技巧。

质量分布原理由弗罗斯特曼(Frostman,O.)于1935年证明，也称为弗罗斯特曼引理。

分形集的豪斯多夫维数的下界的估计一般要比上界的估计困难得多，最常用的技巧是找一个由这个集合所支撑的分布“均匀”的测度，使得它在任何一个球上的质量被球的、维体积所控制，它由下面的质量分布原理所表述：设E⊂Rd上的正有限测度μ满足s阶赫尔德条件，即存在常数c>0，s≥0，δ>0使得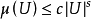对所有满足|U|