[科普中国]-5r覆盖引理

5r覆盖引理（5r-covering lemma）是Rd中的闭球族的一种覆盖定理。

简介5r覆盖引理是Rd中闭球族的一种覆盖定理。

该引理断言：设ℬ为Rd中有界区域内的闭球族，则存在可列或有限个彼此不相交的子球族{Bi}，使得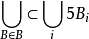其中5Bi表示与Bi同心，半径为Bi5倍的球。1

覆盖覆盖是数学术语，设Ф是拓扑空间X的子集族，称Ф是X的一个覆盖，如果对任意x∈X，x至少包含在Ф的一个成员之中。

维塔利覆盖引理数学上，维塔利(Vitali)覆盖引理是一个组合几何的结果，用于实分析中。这引理说给出一族球，可以从中找到互不相交的球，将这些球半径增加一定倍后，就能把其他的球都覆盖住。

在一个度量空间中有一族闭球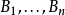，则这一族球中存在互不相交的球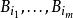，适合条件

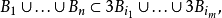
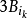表示和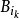有相同中心，而半径是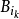的三倍的球。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所