[科普中国]-芒德布罗集

芒德布罗集(Mandelbrot set)是分形几何和复动力学中一个非常有趣而又典型的集合：平方与加法是定义芒德布罗集所需要的程序开始，这实际上就是定义芒德布罗集所需要的一切1。

基本介绍对于二次多项式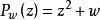 ，芒德布罗集M定义为

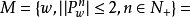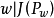{ 是连通集}.

M是闭集且有关系式

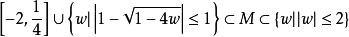M的所有分支都是单连通区域，M的余集是一个区域。杜瓦地(A.Douady)和胡巴特(J.H.Hubbard)于1982年证明了集合M是连通集。富仓光宏(M.Shishikura)证明了M集的边界具有豪斯多夫维数22。

关于芒德布罗集，仍有一些重要的问题未能解决。例如，芒德布罗集是否为局部连通?是否M的每一个分支都是双曲的(即是否每个分支中存在参数w，使得Pw(z)有吸性周期点)?

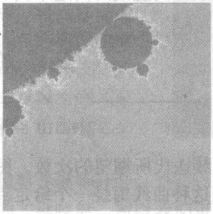
芒德布罗集是最惊人的数学对象之一。图1给出了一个芒德布罗集的图形。仔细观察会发现，每一处边缘都具有“叶子”的特征。留意图1的底部。将其放大，得到图2。现在，新的“叶子”成分出现了。再将图2的底部放大，可观察到图3所示的令人眼花缭乱的结构。图4和图5是放大更多的图形。每副图都显示出了一种丰富的、精细的结构。

|| ||

互联网上有很多计算机程序可用来探索芒德布罗集。(随着图形的放大)越来越精细的结构不断出现。它吸引了数学、物理学和生物学上的顶尖头脑。此外，正如下文所解释的，这种模式是“普遍存在的”。它出现在很多看似无关的系统中。洗牌法和吉尔布雷思原理可用来描述该序列的点的排序方法。

平方与加法从一个简单的程序开始：平方与加法。这实际上就是定义芒德布罗集所需要的程序开始：平方与加法。这实际上就是定义芒德布罗集所需要的一切。

重复平方是人们很熟悉的一个程序。从2开始，我们会依次得到2，4，16，256，65 536，…，直到无穷。从小于1的一个数开始，如1/2，我们会依次得到1/2，1/4，1/16，1/256，1/65 536，…，该数列趋向于0。我们还要处理负数的情形。从一1开始，重复平方，会依次得到一1，1，1，1，1，1，…。如果每一次平方后再加上一个固定的数，事情就会变得更有意思了。假定每次加上1。从0开始，平方后加上1，即02+1=1，重复平方后加上1的过程，依次得12+1=2，22+1=5，52+1=26，…，直到无穷。若每次加上-1，则依次得到0，02-1=-1，(-1)2-1=0，02-1=-1，(-1)2-1=0，…。该数列永远在0和-1之间摆动。若每次加上-2，结果也是类似的，所得数列为0，-2，2，2，2，2，…。加上一个小于-2或者大于0的数，结果都会得到一个趋于无穷的数列。加上一个-2与0之间的数，结果都会得到一个有界数列(随着时间的推移，它们不会离0任意远)。它们都在芒德布罗集里。

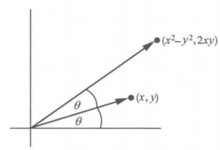
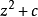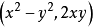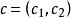平方与加法程序在二维上具有完美的意义，即将点z 变成点。有一个简单的几何意义：二维中的点z 可通过其坐标(x，y)来刻画。图,6给出坐标为(x，y)的一个点以及该点与原点之间的连线，该连线与x轴的夹角为。要得到点(x，y)的平方，可取点(x，y)到原点距离的平方以及夹角的2倍，作出新的点，其坐标为。将其记为。加上得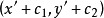。每次使用同一个c值，重复上述程序。从0 开始，若由该程序产生的点位于圆心在原点的足够大的圆内，则将c归人芒德布罗集。

周期点加上某些特殊的数，会得到以一种固定模式循环的数列。假设每次平方后所加的数为c，则所得数列为：

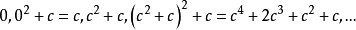若该数列趋向于0，则最终其中一个被迭代的项必定会消失。考虑 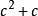这一项，它什么时候等于0?若 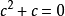，则c=0，或c+1=0即c=-1。上面我们看到，每次加上-1，得到数列0，-1，0，-1，0，-1，…，这是一个“周期为2”的模式。考虑下一项 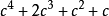。c取何值时它等于0?c=0显然满足，但我们前面已经见过。若 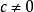，则将各项除以c，考虑 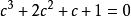。这是一个三次方程，根据复杂的三次方程求根公式，可知在此情况下数值

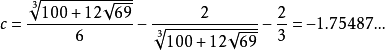满足条件。用这个数作为c，可得

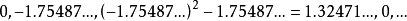该模式会持续出现，每三步重复一次。我们称 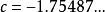为“周期为3”的点。

采用同样的方法，可以得到周期更大的点。例如，将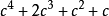 平方后加上c，得到 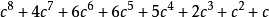。由此得到c的两个新的值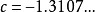： 和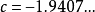 ，两者都是“周期为4”的点。相应的重复数列分别是：

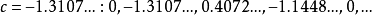
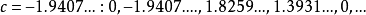对于每个可能的周期，都存在新的周期数列。要找到这些数列，只需求出c的值，使得“平方后加上c”程序的第n次迭代等于0。它们恰好可用吉尔布雷思排列来描述。

完整的芒德布罗集上面所有的活动都局限于一维的直线。而芒德布罗集属于二维。二维上有一个“平方后加上c”的概念，能使重复平方后加上c所得结果有界的c，恰为芒德布罗集上的点。在平面上，c的值是二维的：。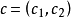

图2给出了芒德布罗集的图形。x轴上介于-2和0之间的值就是上面讨论过的点。中央大心形区域称为心形曲线。它的四周被斑点所包围，而每一个这样的斑点又被更小的斑点所包围(以此类推，直至无穷)。关于芒德布罗集，一个主要的有待研究的问题与c的值有关(现为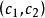)，通过“平方与加法”程序，这些值产生了周期数列。人们猜想，每一个斑点(大斑点，小斑点，以至无穷)都包含一个周期点。这个猜想如果得到了证明，那么，著名的“局部连通性”猜想也就迎刃而解了。

最后，让我们解释一下，芒德布罗集在什么意义下是普遍存在的。对于固定的c，平方与加法程序将x变为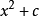。当c变化时，我们得到一族不同的迭代方案。麦克马伦(Curt McMullen)证明，平面上任何一族映射到本身的函数具有芒德布罗集的所有复杂性，包括开口、分形维度和无穷精细性。当然，这也意味着它包含了所有上面所说的吉尔布雷思排列1。

芒德布罗集和茹利亚集分形包括多种处理过程。下面介绍两种与众不同的处理过程。它们能生成具有动态系统特征的图像。动态系统中许多有趣的问题能够通过计算机图形学进行探索3。

假设一系列二次复变函数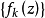 定义为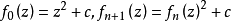 。我们感兴趣的是这个序列随着n值的增加收敛还是发散。有一种直接的检验方法：随着k值的增加，如果 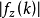有界，则函数集收敛，否则发散。注意，复数由一对实数 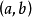定义，通常记为 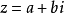，这里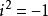 。所以有以下关系式：

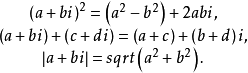
如果将不同的复数c应用于函数序列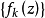 ，且总是从初始值z=0开始，就能研究参数空间{c}的行为。芒德布罗(Mandelbrot)集是一个能让具有这个初始值的函数序列收敛的复数c的集合。如果对于任何k值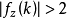， ，那么序列将会发散。所以，只需简单地检查对于k的取值直到一个相当大的数如500时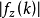， 是否小于2。如果在终止序列之前，发现某个k值使 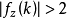，那么对于该复数c，就返回这样的第一个k值；如果没有，那么就返回0。芒德布罗集就是由返回0的复数c组成的集合。

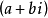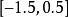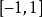为了用图显示这种情况，用2D点(a，b)来表示一个复数 ，根据之前为该复数记录的值，用一个整数渐变色来涂染这个点。也可以采用其他的方法进行标识：每个点定义一个复数，然后运用上面提到的方法来处理这个复数，从而决定点的颜色。这样可以得到一个2D区域，并在该区域上创建一个我们在示例代码中描述的窗口尺寸匹配的网格，运用上面提到的方法处理每一个网格点，然后像之前那样涂染对应的像素。图7显示了一幅芒德布罗集的图像，而右边的细节图像则显示了在一个更小区域内收敛的过程。图中的整个芒德布罗集对应一个a的取值在 ，b在 的复数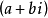 集，而细节区域的取值为 。

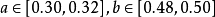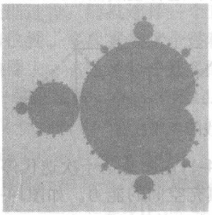
对于这一系列函数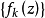，如果改变取固定值和变量的规则，即选择一个固定值c，对于不同的z值计算序列函数，使用和之前相同的着色技术，那么我们可能都会问一个非常相似的问题，即这个序列是否随着n值的增加而收敛或者发散。使得这个序列收敛的复数z的集合称为茹利亚(Julia)集。茹利亚集与芒德布罗集有关，如果用芒德布罗集里的任何一个复数c来生成茹利亚集时，茹利亚集将会连接起来。而如果用芒德布罗集外的一个复数c来生成茹利亚集时，茹利亚集将是完全断开的。用芒德布罗集中非常接近边缘的复数能够生成非常有趣和与众不同的茹利亚集。图8显示由固定点(-0.74543，11301)计算得到的特殊茹利亚集。当然也可以像显示芒德布罗集那样选择其中的一小部分进行显示，给出更为详细和迷人的图像3。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学