[科普中国]-回代过程

定义

设有线性方程组

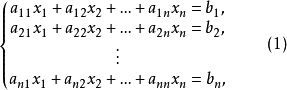或写成矩阵形式

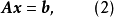其中

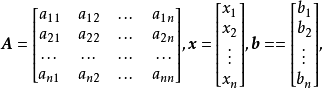设系数矩阵A非奇异(即A可逆)，即A的行列式det(A)≠0，则式(1)有唯一解。

为了对高斯消去法有一个较清楚的了解，先看下列4个未知数的线性方程组的求解过程。

例1 求解线性方程组

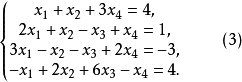
解： 消去法的第1步是用式(1)的第1个方程消去其余方程中的未知数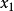，这可分别将第1个方程的-2倍、-3倍和1倍加到第2个~第4个方程上，得

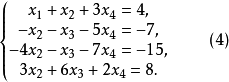第2步是利用式(4)的第2个方程将第3、第4个方程中的未知数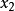消去。为此，可将第2个方程的-4倍和3倍分别加到第3个、第4个方程上，得

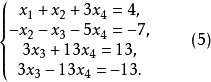第3步是利用式(5)的第3个方程将第4个方程的中的未知数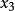消去。为此，可将第3个方程的-1倍加到第4个方程上，得

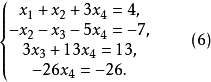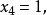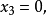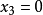到此为止，消元过程结束。并且可以从式(6)的最后一个方程解出将其代入第3个方程可解出再将和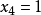代入第2个方程解出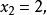最后，将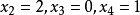代入第1个方程解出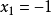。这样就完成了对式(3)的求解，其解为。

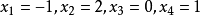以上求解线性方程组的过程称为顺序高斯消去法，其中，利用加减消元法将一般方程组式(3)化为系数矩阵为上三角矩阵的上三角形方程组式(6)的过程称为消元过程，而由式(6)依次求出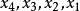称为回代过程。

一般地，顺序高斯消去法主要包含消元和回代两个过程。消元过程就是对式(1)的增广矩阵(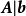)做有限次的初等行变换，使它的系数矩阵部分变为上三角矩阵。所用的初等变换主要是用一个数乘以某一行加到另一行上。1

线性方程组求解线性方程组的求解方法在科学计算中占有极其重要的地位。一方面，在工程技术领域，经常以线性方程组作为其基本模型，例如电学网络问题、热传导问题、质谱仪数据分析、CT图像重建等；另一方面，在许多有效的数值方法中，求解线性方程组是其中的关键步骤，如样条捅值法、矩阵特征值问题、微分方程数值解法等，都离不开线性方程组的求解。

线性方程组的数值解法可分为直接法和迭代法两大类方法。直接法的特点是，运用此类方法求解线性方程组时，如果计算过程中没有舍人误差，那么经过有限次四则运算就能求得式(1)的精确解。但由于实际运算中总有舍人误差，因此直接法求得的解也只能是近似解。另一类是迭代法，它首先选取一组初值，再运用同样的计算步骤，重复计算，求得近似解。由于这类方法中出现了极限过程，因此必须研究迭代过程的收敛性。

求解线性方程组的直接法包括高斯消去法及其变形、直接三角分解法；迭代法包括雅可比迭代法、高斯一塞得尔迭代法和松弛法。直接法的基本思想是利用方程组的变形，逐步将方程组转化为一个简单的、易于求解的特殊形式的线性方程组(如三角形方程组)，然后再求解这一特殊形式的同解线性方程组。高斯消去法便是通过消元过程将方程组约化成上三角形方程组而完成的。1