[科普中国]-阶理想

阶理想是模的算子环的一个单侧理想。设 R 是一个环，当R是交换环时，ann(x)是R的理想，称为x的阶理想（order ideal）。

简介扭模和无扭模

[torsion module and torsion free module]

设 R 是一个环，M 是一个 R 模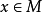， 。定义 R 的左理想 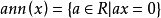。如果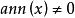 ，称 x 为 M 中的扭元（torsion element）。M中的扭元的集合构成一个子模，称之为M的扭子模（torsion sub-module），记作tor(M)。

若tor(M)=M，则称M为扭模。

若tor(M)=0，则称M为无扭模。

特别地，当R是交换环时，ann(x)是R的理想，称为x的阶理想（order ideal）。1

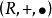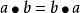交换环设是一个环，如果乘法“”适合交换律，即对任意都有，则称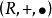是一个交换环，简记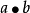为ab。

设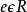，若对任意的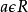都有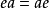，则称e是R的一个单位元，环的单位通常记为1。

例如，整数环ℤ是交换环，数域ℙ上的一元多项式环ℙ[X]也是交换环。

交换代数中讨论的环都是有单位元的交换环，大多数所指的环都是有单位元1的交换环。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学