[科普中国]-力迫关系

力迫关系在力迫法中力迫关系通常记为⊩ （读作力迫），是定义在基础模型 M 中一个二元关系。力迫关系的左变量是一个力迫条件，右变量是力迫语言的句子。

简介力迫关系是一种二元关系，指力迫条件与力迫语句之间的关系。通过力迫定理，它又能反映力迫条件对兼纳模型中的性质的决定关系。对任意偏序集 P，设 p∈P为一个力迫条件，σ为相关的力迫语言中的一个语句， p 与 σ的力迫关系记为p⊩σ，称 p 力迫σ，其定义随力迫法的陈述形式的不同而有较大的差异。

美国数学家科恩(Cohen,P.J.)原来对力迫关系的定义是通过对 σ的结构进行递归定义。现代力迫法通常也采用这种方式定义力迫关系。在布尔值模型中，力迫关系定义为 p⊩σ，当且仅当 e(p)≤||σ||，式中 e 表示 P 到 P 的正规开代数 B=r. o. (P) 的规范嵌入，||σ||表示 σ的布尔值。

力迫关系的左变量是一个力迫条件，右变量是力迫语言的句子。

性质力迫关系具有下列性质:

1.若 p⊩σ， q≤p ，则 q⊩σ。

2.对任何 p∈P，p⊩σ与p⊩⊣σ至多有一个成立.

3.对任何 p∈P，存在 q≤p ，使q⊩σ与 q⊩⊣σ有且仅有一个成立。

4. p⊩⊣σ，当且仅当不存在 q≤p 使q⊩σ 。

5. p⊩σ⋀τ，当且仅当 p⊩σ且 p⊩τ 。

6. p⊢σ⋁τ，当且仅当对任何q≤p，存在 r≥q 使 r⊩σ或 r⊩τ。

由于力迫关系对 ZF 系统的任何模型绝对，因此，它可以在力迫基模型中被定义，由力迫定理可知， ∃p∈G(p ⊩σ)M，当且仅当 M[G]⊩σ，这说明兼纳模型 M[G] 中的性质可以在基模型中通过兼纳集G所决定，这是力迫方法的重要特征。1

力迫定理力迫关系的重要性在于如下的力迫定理 (forcing theorem)：对任意集合论语言的句子φ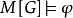， 当且仅当存在 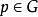使得 。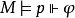

借着力迫定理，泛型扩张M[G] 的性质完全对应于基础模型 M 上关于力迫关系的性质，从而有可能对M[G] 的性质在 M 中作推断。2

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学