[科普中国]-形式伴随方程

形式伴随方程（formal adjoint equation）是在Rn中为确定常数变易公式的积分核而导出的相关方程。

简介概述形式伴随方程是在Rn中为确定常数变易公式的积分核而导出的相关方程。

具体内容设线性泛函微分方程ẋ(t)=L(t,xt)或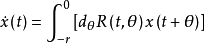的解整体存在，ẋ(t)=L(t,xt)+f(t)的解x(t,σ,φ,f)由常数变易法可用齐次方程的解x(t,σ,φ)和U(t,s)表示为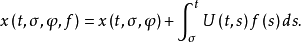当U(t,s)用一途径确定时，导出方程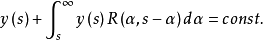

上式的矩阵解Y(s,t)满足：U(t,s)=Y(s,t)几乎处处成立，且上式称为原方程的形式伴随方程。1

常数变易公式常数变易公式是常微分方程的常数变易法在线性泛函微分方程的推广。在拉普拉斯变换表示之下，由通解同样可以得出常数变易公式。

设齐次线性与非齐次泛函微分方程ẋ(t)=L(t,xt)，ẋ(t)=L(t,xt)+f(t)，过(σ,φ)∈R×C的解整体存在，记x(t,σ,φ)为ẋ(t)=L(t,xt)的解，x(t,σ,φ,f)为ẋ(t)=L(t,xt)+f(t)的解，则有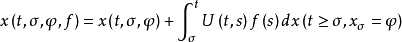当t≥σ时几乎处处成立，并称为常数变易公式。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学