[科普中国]-拉兹密辛条件

拉兹密辛条件是一种表述泛函微分方程的李亚普诺夫稳定性条件。条件的成功之处在于它并没有对方程自身附加新的限制。

简介拉兹密辛条件是一种表述泛函微分方程的李亚普诺夫稳定性条件。

20世纪50年代，当人们把常微分方程的李亚普诺夫方法推广到泛函微分方程时发现，所有的稳定性定理的适用范围都极其有限。例如，对最简单的方程ẋ(t)=a(x)t+bx(t-τ)(τ=const>0)，取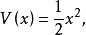 则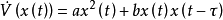 中第二项是否恒正或恒负难以确定。

拉兹密辛(Razumikhin,B.)注意到并不需要在原点的邻域内定号，只要当|x(t-τ)|≤|x(t)|时定号即可，这就是拉兹密辛条件。

推广拉兹密辛条件还可推广为P(x(s))≤P(x(t))(s≤t,t≥σ)。P(ξ)是K类函数：P(0)=0，P(ξ)>0(ξ≠0)。在这个条件之下，上述方程中只要a0，w(s)>0，且存在连续函数P(s)>0，s>0，条件2换为V(t+θ,x(t+θ))≤P(V(t,x(t)))(θ∈[-r,0])，则方程的解是一致渐近稳定的。1

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学