[科普中国]-庞特里亚金定理

庞特里亚金定理是关于滞后型线性自治系统特征根分布的一个重要定理。是1942年庞特里亚金在理论上给出的准则。

简介庞特里亚金定理是关于滞后型线性自治系统特征根分布的一个重要定理。

线性自治常微分方程的特征根全部分布在虚轴左边的充分必要条件是众所周知的劳斯-霍维茨判据。对滞后型线性自治系统是否有类似的准则?1942年，庞特里亚金在理论上给出了这种准则，这就是庞特里亚金定理。

具体内容把线性自治差分微分方程的特征方程写成H(z)=h(z,ez)=h(z,t)，设诸项中z的最高次数为r，t的最高次数为s，若a≠0，则azrts称为h(z,t)的主项。再记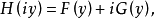则庞特里亚金定理断言：

1、若h(z,ez)有主项，则它的所有零点均具负实部的充分必要条件是，F(y)和G(y)的根都是实的，并且有一个y的值使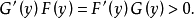

2.若h(z,ez)没有主项，则h(z,ez)必存在具任意大实部的零点。

意义庞特里亚金定理的第二部分证明了超前型与混合型系统的零解必定是不稳定的这一事实。第一部分给出滞后型系统零解渐近稳定的充分必要条件。

但对中立型系统，判断特征根均具负实部这一点并不能保证渐近稳定性。必须指出，庞特里亚金定理的条件是超越的，难以检验的，从应用的角度看，特征根分布的代数判断准则是目前亟待研究的课题。1

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学