[科普中国]-更新方程

更新方程是一类特殊的泛函微分方程，在生态系统中用斯蒂尔杰斯积分表示的滞后型泛函微分方程称为更新方程。

简介更新方程是更新函数满足的一类方程。

更新过程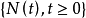 的更新函数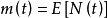 所满足的方程

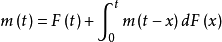被称为更新方程。

更为一般的，对于已知函数 及分布函数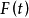，如果未知函数 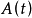满足积分方程

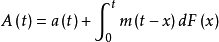因此积分方程就被称为更新方程。这里需要注意的是函数所代表的含义已经被推广，可以是剩余寿命的函数、也可以代表具体问题中的某个期望值函数等等。当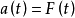 时就是原来定义的更新方程。

人们对更新方程最为关心的问题有：在什么条件下方程的解存在且唯一，以及解具有什么性质等等。1

更新密度更新密度(renewal density)是一种导数。更新函数的导数：

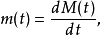称为更新密度。它有如下的概率解释：对于很小的Δt>0，m(t)Δt近似地给出在区间(t，t+Δt)中的平均更新次数。

更新函数更新函数是一种数学期望。更新过程{N(t)，t≥0}在区间(0，t]中的更新次数的数学期望M(t)=E[N(t)](作为变元t的函数)称为更新函数。

本词条内容贡献者为:

何星 - 副教授 - 上海交通大学