[科普中国]-莫尔斯-斯梅尔系统

莫尔斯-斯梅尔系统(Morse-Smale system)是最早得到的一类结构稳定系统。这类系统有一特性：它的非游荡集仅由有限个数的周期元素组成，对这类系统的研究是从1937年获得的庞特里亚金-安德罗诺夫定理的结论开始的，它的通常定义如下：设M是紧致黎曼流形，X是M上的Cr向量场，如果：1.X有有限个奇点和周期轨道，它们都是双曲的；2.若σ1和σ2是X的奇点或周期轨道，那么σ1与σ2的稳定流形与不稳定流形是横截相交的；3.非游荡集Ω(X)恰是X的奇点和周期轨道，则称X是莫尔斯-斯梅尔向量场。完全类似地可给出莫尔斯-斯梅尔微分同胚的定义。动力系统理论已经证明：任何紧致微分流形上都存在莫尔斯-斯梅尔系统，这个重要事实是由莫尔斯(H.M.Morse)及斯梅尔(S.Smale)得到的，故这一类系统通常就以他们的名字命名1。

定义定义1 设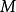为紧致微分流形，令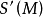表满足如下称为莫尔斯-斯梅尔(Morse-Smale)条件的一切向量场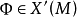之集：

1. 非游荡集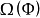是有限多个临界点和有限多条闭轨之并；

2. 所有临界元素均为双曲的；

3. 临界元素的稳定流形与不稳定流形横截相交。

向量场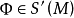称为莫尔斯-斯梅尔(简记为M-S)向量场。

定义2微分同胚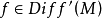称为莫尔斯-斯梅尔(简记为M-S)微分同胚，需满足如下条件：

1. 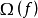是有限集；

2. 所有周期点都是双曲的；

3. 周期点的稳定和不稳定流形横截相交。

所有M-S微分同胚的集合，记为。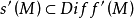

定义3 设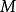是紧致微分流形，与是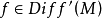的双曲周期轨道[对应的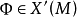，的双曲临界元素]，若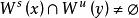，则称前于，记为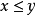，对M-S微分同胚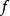[对应的M-S向量场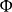]的全体周期轨道[对应的全体临界元素]配上关系“≤”为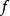[对应的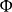]的骨架图。

命题4 上述关系≤是相应集合上的偏序关系2。

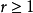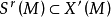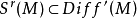相关定理定理1(帕利斯(Palis)) 1. 对，为开集；为开集；

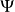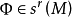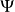2. 若向量场充分邻近于由，则与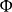有同构的骨架图；对应地，当微分同胚g充分邻近，则g与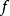有同构的骨架图。

定理2对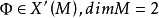，则M-S条件等价于下列条件：

1. 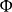的一切轨道的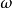极限集与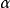极限集均为临界元素；

2. 所有临界元素是双曲的；

3. 无鞍点间的连接轨道。

定理3 (Peixoto)设M为紧致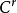二维可定向流形(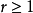)，当且仅当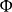是M-S向量场时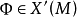，为结构稳定。

定理4 (帕利斯-斯梅尔)每一微分同胚是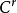结构稳定的，每一个向量场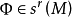是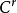结构稳定的2。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学