[科普中国]-点态退化系统

点态退化系统是值域不能充满方程定义域的泛函微分方程。对于泛函微分方程，即使是线性自治系统也可能点态退化。

简介点态退化系统是值域不能充满方程定义域的泛函微分方程。

设RFDE(f)过(σ,φ)的解整体存在且惟一，对给定的σ∈R，∀φ∈C，若存在Rn的真子空间，t1>σ，使得方程的一切解x(t,σ,φ)成立x(t1,σ,φ)∈（对∀φ∈C），则称方程在t1处点态退化，反之称点态完备。

若∀t1∈I⊂R点态退化，则称方程在I上点态退化。

实例例如方程ẋ(t)=-α(t)x(t-1)，其中当t≥σ+3时，x(t,σ,φ)≡0对∀σ∈R，φ∈C成立。

性质由于常微分方程的解映射定义了一个同胚，即解映射之下空间Rn的球的像含有一个球，所以它总是点态完备的。而对于泛函微分方程，即使是线性自治系统也可能点态退化。

例如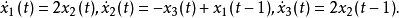设σ=0，∀φ∈C（[-r,0],R3），当t≥1时x(t,σ,φ)=(x1,x2,x3)T都落在同(1,-2,-1)T垂直的平面上。但对线性自治系统可以证明：若n≤2，则单滞量的情形，系统是点态完备的，而n=2且有两个滞量的情形，则存在点态退化的例子。

对线性自治系统还可以证明，若系统在t*处点态退化，则∀t≥t*，系统也点态退化。1

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学