[科普中国]-反向延拓定理

反向延拓定理断言：由滞后型泛函微分方程初值问题的提法，它总是沿正向(t≥σ)求解的，仅当方程满足某些特定条件时，对某些初始函数可以进行负向延拓(t≤σ)。

简介反向延拓定理是一种微分延拓。

由滞后型泛函微分方程初值问题的提法，它总是沿正向(t≥σ)求解的，仅当方程满足某些特定条件时，对某些初始函数可以进行负向延拓(t≤σ)。

实例例如，当f和φ满足下列条件时，方程ẋ(t)=f(t,xt)的初值问题的解是可以负向延拓的（负向延拓亦称反向延拓），并有以下重要结论：

1.存在α∈(0,r)，使得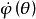 在[-α,0]上连续，且满足 ；

2.设Ω⊂R×C，f:Ω→Rn关于φ有二阶连续的弗雷歇导数，并且在Ω上于-r处是原子的，

则∃ᾱ(α)>0，使方程过(σ,φ)的解在[σ-r-ᾱ,σ]上存在且惟一。1

延拓函数的延拓：设E与F为两个集合，P为E的子集，而f为从P到F中的映射. 任一从E到F中的映射，如果它在P上的限制为f，则称该映射为f在E上的延拓。

解的延拓：不能继续延拓的解称为饱和解，饱和解的存在区间称为解的最大存在区间。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学