[科普中国]-科恩条件

科恩条件是判定尺度函数正交性的一个条件，这个条件是科恩(Cohen,A.)于1990年提出的。

简介概述科恩条件是判定尺度函数正交性的一个条件，这个条件是科恩(Cohen,A.)于1990年提出的。

具体内容对于一个紧集K，如果|K|=2π，且对任意ξ∈[-π,π]都存在l∈Z，使ξ+2πl∈K，那么称K为与[-π,π]是2π-同余的。对于m0(ξ)∈C[-π,π]，如果存在与[-π,π]同余的紧集K，K以O为内点，以及常数C0>0，使得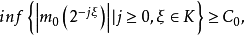那么称m0(ξ)满足科恩条件。1

正交性“正交性”是从几何中借来的术语。如果两条直线相交成直角，他们就是正交的。用向量术语来说，这两条直线互不依赖。沿着某一条直线移动，该直线投影到另一条直线上的位置不变。

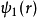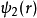如果两个函数和满足条件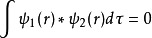：，则称这两个函数相互正交。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学