[科普中国]-按一次近似决定稳定性

按一次近似决定稳定性(stability in the first approximation)是应用近似的线性系统研究更复杂系统稳定性的一种方法，即由最基本的线性(一次)系统出发研究能否决定更复杂系统的稳定性。

基本介绍对于常系数线性方程组

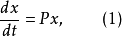其解的渐近性态是很清楚的。如果在(1)的右端加上一个小扰动，即

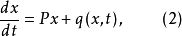则人们试图从(1)的解的已知性态去获得(2)在原点附近的渐近性态，这就是通常所称的按一次近似决定稳定性的问题1。

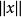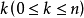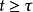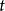相关结论当P没有零或纯虚数的特征根，且q相对于 适当小时，则(1)和(2)在原点附近解的渐近性态完全相同。设P有 个具有负实部的特征根，而其余具有正实部，又假定当 及 时，对 一致地有

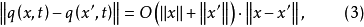则存在常数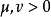，使得下述性质成立：

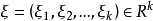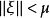1. 当且时，(2)有连续依赖于ξ的解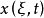，使得

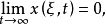且原点关于这族解是渐近稳定的。

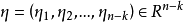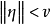2. 当且时，(2)有连续依赖于η的解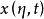，使得

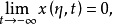设(2)为自治的：，且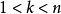，则性质1和2表现的性质为典型的鞍点性质，它们给出了原点的局部稳定和不稳定流形1。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学