基本介绍定理
(庞加莱-本迪克松定理) 考虑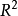 上的微分方程
上的微分方程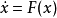 。
。
(a)假设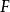 在
在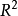 上有定义,正半轨
上有定义,正半轨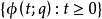 有界,则
有界,则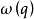 :(i)含有不动点或(ii)是周期轨。
:(i)含有不动点或(ii)是周期轨。
(b)假设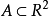 是有界闭子集且是微分方程的正不变集,假设
是有界闭子集且是微分方程的正不变集,假设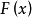 在
在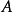 内有定义,但没有不动点,则对任意的
内有定义,但没有不动点,则对任意的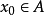 ,轨线
,轨线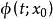 :(i)是周期轨或(ii)趋于一个周期轨( 当
:(i)是周期轨或(ii)趋于一个周期轨( 当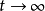 时)且
时)且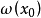 就是该周期轨。
就是该周期轨。
注意点注1要使平面上的连通区域A既是正不变集又不含有不动点,则它必是含有一个“洞”的环域,这样它就有两条边界,每一边界都是闭曲线(不必是圆)。
注2为使环域A成为正不变集,只需系统的向量场在边界上指向环域内部。
注3对上述定理可做适当的变动,即环域A是负不变集,边界上的轨线都进入A的外部2。
证明思路这里叙述证明的关键思路,证明需要利用流关于初始值的连续性。
轨线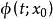 正向位于A内,势必不断地接近于某点z,即存在时间序列
正向位于A内,势必不断地接近于某点z,即存在时间序列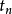 使得
使得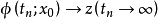 。这种思想就是数学中的紧性,类似于有界递增点列一定收敛,于是
。这种思想就是数学中的紧性,类似于有界递增点列一定收敛,于是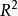 中的有界点列必须趋近于某点。点z不是不动点,其附近的轨线大致有相同的走向。设
中的有界点列必须趋近于某点。点z不是不动点,其附近的轨线大致有相同的走向。设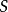 为过点z的截线,使得附近其他轨线同向穿过S,则对于充分大的n,总可以调节
为过点z的截线,使得附近其他轨线同向穿过S,则对于充分大的n,总可以调节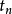 使得
使得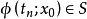 。取一段轨线
。取一段轨线
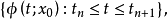 以及S上
以及S上 与
与 之间的线段
之间的线段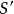 ,它们构成一条闭曲线
,它们构成一条闭曲线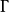 ,该闭曲线将
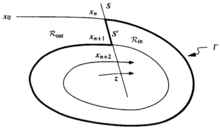
,该闭曲线将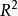 分成两部分(参见图1)。从
分成两部分(参见图1)。从 出发的轨线要么进入
出发的轨线要么进入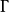 的外部,要么进入
的外部,要么进入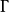 的内部;而从
的内部;而从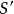 上任一点出发的轨线具有相同的性态。因此当
上任一点出发的轨线具有相同的性态。因此当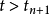 时
时 不可能重新进入其他区域,这意味着轨线与S的交点呈现单调性,它们必从一侧收敛于z。进一步分析表明,如果z不是周期的,则附近的轨线不可能返回,故z必须是周期的。
不可能重新进入其他区域,这意味着轨线与S的交点呈现单调性,它们必从一侧收敛于z。进一步分析表明,如果z不是周期的,则附近的轨线不可能返回,故z必须是周期的。
由上述证明可在收敛于周期轨方面获得更多的认识,实际上,若一条轨线在极限环的一侧聚集,则庞加莱映射在该侧是单调且吸引的。这说明极限环该侧附近的轨线的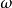 极限集就是该极限环,极限环在该侧是轨道渐近稳定的。如果周期轨两侧的轨线的
极限集就是该极限环,极限环在该侧是轨道渐近稳定的。如果周期轨两侧的轨线的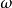 极限集都是该周期轨,则该周期轨就是(两侧)轨道渐近稳定的,即有下述推论2。
极限集都是该周期轨,则该周期轨就是(两侧)轨道渐近稳定的,即有下述推论2。
推论推论 考虑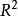 上的微分方程
上的微分方程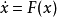 ,假设
,假设 为孤立的周期轨。
为孤立的周期轨。
(a) 假设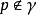 且以
且以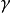 为其
为其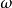 极限集,即
极限集,即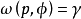 ,则对于充分靠近
,则对于充分靠近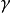 且与p位于
且与p位于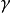 同侧的点q,有
同侧的点q,有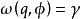 ,即
,即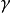 为单侧轨道渐近稳定的;
为单侧轨道渐近稳定的;
(b) 假设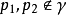 ,
, 位于
位于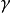 的不同侧,且
的不同侧,且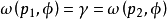 ,则
,则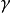 是轨道渐近稳定的(双侧)2。
是轨道渐近稳定的(双侧)2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国