[科普中国]-极限集理论

极限集理论是定性理论的重要基础之一。对于平面定常系统，极限集理论有甚为清晰完整的结论。

简介极限集理论是定性理论的重要基础之一。

ω极限集考虑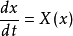系统或平面系统。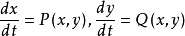

从x0点出发的轨线φτ(x0)，若存在序列tn→+∞，使得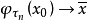，则称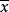为轨线φτ(x0)的ω极限点，称φτ(x0)的所有ω极限点的集合为φτ(x0)的ω极限集，记为Lω(x0)。

α极限集类似地，考察t→-∞的情况，则可得出α极限点与α极限集的定义。φτ(x0)的α极限集记为Lα(x0)。

结论由上述定义易见，奇点x0是φτ(x0)=x0的惟一的ω和α极限点，闭轨φτ(x0)上的任一点都是此闭轨的ω和α极限点。亦即，奇点和闭轨分别为它们自身的ω和α极限集。

对于平面定常系统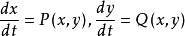，极限集理论有甚为清晰完整的结论，可归结如下：若系统的一条正半轨φτ(x0)(t≥0)保持在有界区域D内，则Lω(x0)必属于下列情形之一：

1一个奇点；

2一条闭轨；

3一条奇闭轨。

由此即可推出庞加莱-本迪克松定理。1

定性理论定性理论又称“微分力一程定性理论”，“几何理论”，是根据全而分析微分力一程所确定的积分曲线的整体分布状况来研究解的性质的理论。

迄今定性理论仍以二阶为主，主要内容是分析奇点，极限环的个数，位置和轨线的走向。在力学，天体力学等工程技术领域有广泛的应用。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学