[科普中国]-闭轨

闭轨（close orbit）是微分方程的周期解在相空间上所对应的一条封闭曲线。

简介闭轨是微分方程的周期解在相空间上所对应的一条封闭曲线。

对系统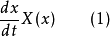的解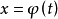，如果φ(t)的各个分量均为t的具有相同最小周期的周期函数，则称此解为周期解，它在相空间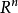内对应于一条闭曲线L，称为(1)的一条闭轨。

性质孤立的闭轨就称为极限环。

所谓孤立，即指存在L的邻域U，使在U内不存在(1)的其他闭轨，且对 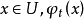或者当 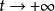时趋于L，或者当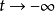时趋于L。

与闭轨以及极限环密切相关的奇闭轨是指由若干奇点和两端进入奇点(当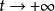或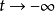)的轨线所构成的单闭曲线。若其上只含一个奇点，则称为同宿奇闭轨；若其上含多于一个奇点，就称为异宿奇闭轨。

对n=2时的平面系统

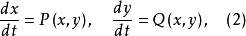由于在(x,y)平面上，有若尔当曲线定理，故可对其极限环以至极限集的性态作深入的分析研究。

推广(2)的极限环L将其邻域U分为内外两侧，若两侧的轨线当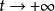(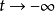)时均盘旋逼近L，则称L为稳定（不稳定）极限环；若一侧轨线当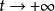时盘旋逼近L，另一侧当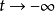时盘旋逼近L，则称L为半稳定极限环1

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学