正线性算子逼近(approximation by positive linear operators)是一类常用的逼近,设f∈C[a,b],如果对一切x∈[a,b]都有f(x)≥0,则记f≥0,设L是C[a,b]到C[c,d]的线性算子,[c,d]⊂[a,b],如果对f≥0有L(f)≥0,则称L为正线性算子。此时,用L(f,x)在[c,d]上逼近f(x)称为正线性算子逼近。
基本介绍正线性算子逼近是一类常用的逼近。设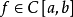 ,如果对一切
,如果对一切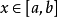 都有
都有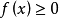 ,则记
,则记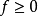 。设L是
。设L是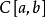 到
到 的线性算子,
的线性算子, 如果对
如果对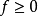 有
有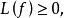 则称L为正线性算子,此时,用
则称L为正线性算子,此时,用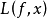 在
在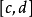 上逼近
上逼近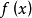 称为正线性算子逼近。设
称为正线性算子逼近。设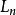 是
是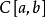 到
到 的正线性算子,
的正线性算子, 如果对于
如果对于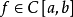 ,
,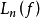 都是
都是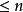 次代数多项式,那么
次代数多项式,那么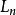 称为n阶正多项式算子。用这种算子在
称为n阶正多项式算子。用这种算子在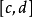 上逼近函数,其临界阶是
上逼近函数,其临界阶是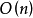 。事实上,记
。事实上,记 那么至少有一个
那么至少有一个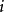 使得
使得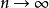 时,
时,
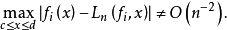 这是科罗夫金(Коровкин,Π.Π.)证明的。对于
这是科罗夫金(Коровкин,Π.Π.)证明的。对于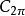 的情形,有类似的概念与结论,只是代替n次代数多项式是n阶三角多项式,而三个试验函数是1,cos x及sin x,正是由于正多项式算子的逼近阶不高于n,所以正多项式算子虽然是一种良好的逼近方法,但其应用还是有局限性的,不能像代数多项式逼近连续函数那样,其最佳逼近的阶会随被逼近函数光滑性增加而提高。
的情形,有类似的概念与结论,只是代替n次代数多项式是n阶三角多项式,而三个试验函数是1,cos x及sin x,正是由于正多项式算子的逼近阶不高于n,所以正多项式算子虽然是一种良好的逼近方法,但其应用还是有局限性的,不能像代数多项式逼近连续函数那样,其最佳逼近的阶会随被逼近函数光滑性增加而提高。
相关定理为了证明正线性算子序列的一致收敛,只需证明它对于几个具体的函数一致收敛即可,这就是
定理1 设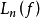 是
是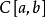 中的正线性算子序列,如果对于
中的正线性算子序列,如果对于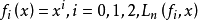 在
在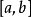 上一致收敛于
上一致收敛于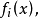 则对于每个函数
则对于每个函数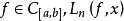 在
在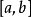 上一致收敛于
上一致收敛于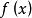 。
。
定理2 设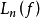 是
是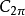 中的正线性算子序列,如果对于
中的正线性算子序列,如果对于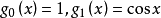 和
和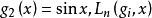 在全实轴上一致收敛于
在全实轴上一致收敛于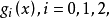 则对于每个函数
则对于每个函数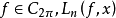 在全实轴上一致收敛于
在全实轴上一致收敛于 。
。
性质(A) 记S是紧致度量空间,设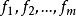 是定义在S上的m个连续实函数,如果存在m个连续的实函数
是定义在S上的m个连续实函数,如果存在m个连续的实函数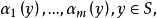 使得在S上,
使得在S上,
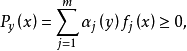 并且,当且仅当
并且,当且仅当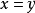 时,
时,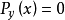 ,则说
,则说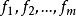 具有性质(A)。
具有性质(A)。
定理3 设函数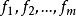 满足条件(A),
满足条件(A), 是映照
是映照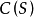 到其自身的正线性算子序列,如果在S上
到其自身的正线性算子序列,如果在S上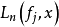 一致收敛于
一致收敛于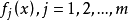 ,则对于任一
,则对于任一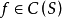 ,
,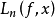 在S上也一致收敛于
在S上也一致收敛于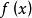 。
。
定理4 设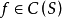 ,则
,则 在S上一致收敛于
在S上一致收敛于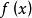 。
。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国