概念
设 为欧氏空间
为欧氏空间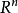 中的单位球面,
中的单位球面,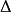 为
为 上的
上的 算子,则根据椭圆算子的性质有
算子,则根据椭圆算子的性质有
引理1:存在 上的
上的 函数系
函数系 ,它满足:
,它满足:
(1) 形成
形成 中的完全标准正交系;
中的完全标准正交系;
(2)每个 均为
均为 的特征函数:
的特征函数: ;且当
;且当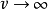 时,
时, 对某个正数
对某个正数 成立。
成立。
**引理2:**设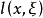 是
是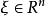 的齐
的齐 次函数,当
次函数,当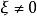 时,关于
时,关于 为
为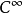 ,且所有的
,且所有的 关于
关于 属于
属于 ,则有球面调和分解
,则有球面调和分解
 式中
式中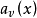 为
为 函数,
函数,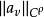 关于
关于 速降。
速降。 为齐
为齐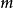 次,在
次,在 时属于
时属于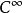 ,而且对任意
,而且对任意 ,
, 关于
关于 是缓增的。1
是缓增的。1
基本原理设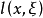 满足引理2中的条件,算子
满足引理2中的条件,算子 按下式定义:
按下式定义:
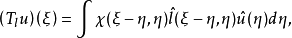 其中
其中 为
为 关于
关于 的傅里叶变换,则称
的傅里叶变换,则称 是以
是以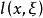 为象征的仿微分算子。
为象征的仿微分算子。
若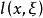 为有限项满足引理2中的条件的函数之和,
为有限项满足引理2中的条件的函数之和, ,则
,则 可相应地定义为
可相应地定义为 。
。
由此可知,当象征 与
与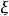 无关时,仿积就是一类特殊的仿微分算子。此外,如果在
无关时,仿积就是一类特殊的仿微分算子。此外,如果在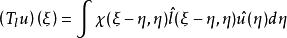 式子右边略去截断函数
式子右边略去截断函数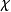 ,则积分
,则积分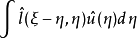 正是一个拟微分算子
正是一个拟微分算子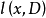 作用于
作用于 以后的傅里叶变换。所以,仿微分算子可以视作拟微分算子经过了某种“修正”而来,然而正是这一修正使仿微分算子在非线性偏微分方程的研究中发挥了重大的作用,也正是由于这一修正,我们得重新详细地考察这类算子的运算法则以及算子运算和象征运算之间的关系。1
以后的傅里叶变换。所以,仿微分算子可以视作拟微分算子经过了某种“修正”而来,然而正是这一修正使仿微分算子在非线性偏微分方程的研究中发挥了重大的作用,也正是由于这一修正,我们得重新详细地考察这类算子的运算法则以及算子运算和象征运算之间的关系。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国