超几何方程具有三个正则奇点并有规范形式的一类富克斯方程。利用(非奇)分式变换v= (AC-BD≠0),对具有三个正则奇点的富克斯方程进行变量代,可以进一步化简方程。
定义二阶线性微分方程
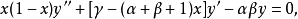 其中
其中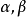 和
和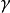 为任意参数,被称为超几何方程.它在x=0,x=1和
为任意参数,被称为超几何方程.它在x=0,x=1和 有奇点.
有奇点.
此外,任意齐次线性二阶微分方程
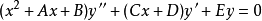 可被转换为超几何方程,前提是方程
可被转换为超几何方程,前提是方程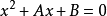 有两个不同的根
有两个不同的根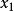 和
和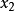 .重写上述超几何方程在如下定义的新的自变量t下
.重写上述超几何方程在如下定义的新的自变量t下
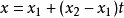 得
得
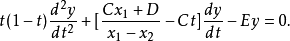 其中设
其中设
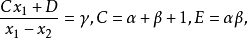 再次用x表示新变量t 即得到超几何方程.
再次用x表示新变量t 即得到超几何方程.
如果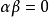 则超几何方程通过两次积分是可解的.如
则超几何方程通过两次积分是可解的.如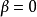 并积分方程
并积分方程
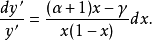 得到
得到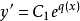 ,其中
,其中
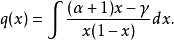 则二次积分得到
则二次积分得到
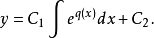
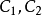 均为常数。
均为常数。
在超几何方程理论中,主要强调的是超几何方程的渐近线和它在单点旁的级数解.但是,实际上经常需要一类超几何方程的通解解析式.因此,下面的定理决定了一类超几何方程可以被初等函数可积或是求积.1
相关定理超几何方程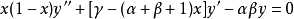 在
在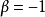 和两个任意参数
和两个任意参数 和
和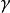 :
:
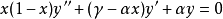 的通解能通过积分得到,其形式是
的通解能通过积分得到,其形式是
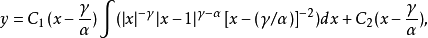 其中
其中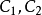 是任意常数。
是任意常数。
注: 如果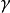 和
和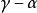 是有理数,可以通过标准变换将上式中的积分化简为有理函数的积分并将上式的解表示为初等函数.1
是有理数,可以通过标准变换将上式中的积分化简为有理函数的积分并将上式的解表示为初等函数.1
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国