概述
非线性泛函分析已成为现代数学中的一个重要分支,并且在其他分支中发挥重要作用,非线性泛函分析是处理非线性问题的重要有力工具,尤其是处理应用中出现的大量微分方程中发挥不可替代的作用在非线性泛函分析中,用锥理论半序方法来处理方程是直观而又实用的方法,并和拓扑方法相结合有力的推动了现代非线性泛函分析的发展在这方面,很多专家都取得了辉煌的成就其中,非线性边值问题来源于应用数学和物理的多个分支,是分析数学中研究最为活跃的领域之一。非线性泛函分析理论能够成熟的运用于解决非线性微分边值间题中去,并把解的存在性转化为某个非线性算子的不动点存在性本文利用锥理论,不动点定理等研究了几类微分方程奇异边值间题解的情况,得到了一些新成果。
利用正交射影方法(变分方法)来研究非线性边值问题
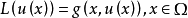
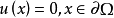
其中L是所谓的场位偏微分运算子。1
非线性场位运算子方程假设H是实Hilhert空间,H'为其共扼空间,H上的内积和范数分别表示为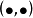 和
和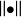 ,而H'上的范数表示为
,而H'上的范数表示为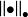 ,此外,H’和H的共扼对表示为
,此外,H’和H的共扼对表示为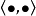 ,我们要研究的是H上的非线性方程:
,我们要研究的是H上的非线性方程:
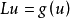
其中L是由H到H’里的非线性运算子,且L(0)=0,而g(u)是定义在H上的泛函数。
定义:
L称为场位运算子,假如存在一个定义在H上的泛函数F(u),此泛函可微,即
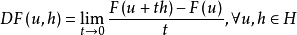
而且,
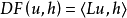
若L是一个场位运算子,则称此方程为场位运算子方程。
令
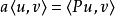
考虑下面两个变分形式的问题:
变分问题一:
寻找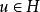 ,使得泛函
,使得泛函
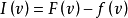
在H上取极小值,其中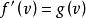
注意,在场位运算子的定义里,泛函F(u)可以相差一个常数项,因此通过常数项的适当选择,不失一般性,今后总假设F(0)=0。
变分问题二:
寻找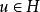 ,使得成立
,使得成立
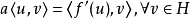
变分原理运算子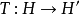 称为非单调的,假如对于任意
称为非单调的,假如对于任意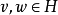 ,成立不等式
,成立不等式
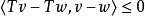
定义在H上的非线性泛函f(v)称为凹泛函数,假如对于任意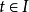 以及
以及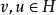 ,有
,有
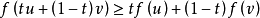
引理1设非线性泛函数f(v)可微,则f(v)是凹泛函数的必要充分条件是,f(v)的微分f'(v)是非单调的
引理2(1)设L是场位运算子,则有等式
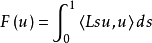
(2)设L是弱可微的运算子,则
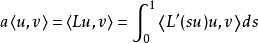
定理1假设定义在H上的非线性泛函f(v)存在微分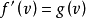 ,而且微分
,而且微分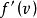 是非单调的。此外,再设场位运算子
是非单调的。此外,再设场位运算子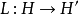 满足下面的条件:
满足下面的条件:
(1)L是弱连续弱可微的;
(2)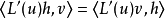
(3)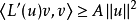
解的唯一性和存在性我们要讨论运算子方程的解存在问题以及唯一性问题,解的唯一性是很显然的,事实上,设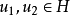 ,则有
,则有
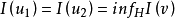
因为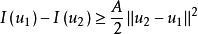
所以
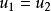




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国