[科普中国]-连续窗口傅里叶变换

连续窗口傅里叶变换亦称短时傅里叶变换，它是在傅里叶变换积分表达式的被积函数之中加上一个窗口函数而成的。

简介连续窗口傅里叶变换亦称短时傅里叶变换，它是在傅里叶变换积分表达式的被积函数之中加上一个窗口函数而成的，通过重构公式它可以表示平方可积函数。

给定一个窗口函数g(t)∈L2(R)，人们把关于窗口函数g(t)的在L2(R)上的连续窗口傅里叶变换定义为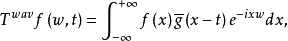其中w,t∈R，f(x)∈L2(R)。

实例例如，取g为高斯函数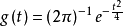Twavf在点(w,t)的值反映了f在时间t，频率w点的局部信息。1

傅立叶变换傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所