[科普中国]-伴随微分方程

简介

伴随微分方程(adjoint differential equation)是与给定微分方程有共扼关系的微分方程。对n阶齐次线性常微分方程

称

为式(1)的伴随微分方程，称M[y]为L[y]的伴随微分式。反之，L[y]也是M[y]的伴随微分式。在伴随微分式之间成立等式

这里N(y,z)是 的双线性型

等式(3)称为拉格朗日恒等式。等式(4)称为拉格朗日双线性型。如果能得到M[y]=0的p个独立解，就可把原来方程L[y]=0的阶数降低p阶。当 时，就称L[y]=0是自伴的(微分方程)。

对齐次线性一阶常微分方程组

称方程组

为方程组(5)的伴随微分方程组。1

辨识算法与伴随微分方程的关系考虑如下微分方程

如果，，则称DC为微分方程的不变集（invariant set）；如果，则称为微分方程的平衡点，显然；如果，则称DA为微分方程的吸收域（domain of attraction），显然DC⊂DA。如果“DA严格大于DC”，则DC是稳定不变集；如果“为DA全平面”，则微分方程是DC的“整体渐近稳定”。如果存在函数V(x)>0，∀ x，且V(x)是递减的，即

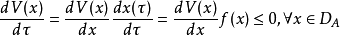及

则称V(x)为微分方程的Lyapunov函数。也就是说，如果存在满足上述两式的函数V(x)，则微分方程时稳定的。

基于上述微分方程的稳定性概念，Ljung给出了关于辨识算法收敛性与伴随微分方程稳定性之间的联系：

（1）设DC是伴随微分方程的不变集，且DA为相应的吸收域，若辨识算法 （“充分经常，sufficiently often”），则模型参数估计值 。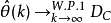

（2）伴随微分方程的平衡点可能是辨识算法的收敛点。

（3）伴随微分方程 的运动轨迹是辨识算法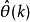 的渐近运动路径。2