[科普中国]-n阶线性常微分方程

n阶线性常微分方程（linear differential equation of n-th order）是未知函数导数最高阶数为n的线性常微分方程。

简介n阶线性常微分方程是未知函数导数最高阶数为n的线性常微分方程。

如果方程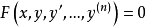的左端函数F包含的未知函数及其各阶导数都是一次的，则称方程为n阶线性（常微分）方程。

一般形式n阶线性常微分方程的一般形式可表为

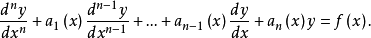
当f(x)≢0时，方程称非齐次方程；当f(x)=0时，则称为齐次方程。1

线性常微分方程线性常微分方程是微分方程中出现的未知函数和该函数各阶导数都是一次的，称为线性常微分方程。它的理论是常微分方程理论中基本上完整、在实际问题中应用很广的一部分。

一阶线性微分方程的多种解法及其教学问题：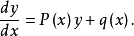

对应的齐次线性方程为 ：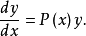

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学