定义
线性微分方程组是具有完整构造性质和广泛应用的一类常微分方程组,如果方程组
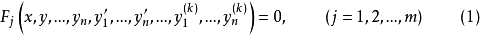 的左端各函数
的左端各函数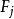 包含的各未知函数及其各阶导数都是一次的,则称方程组(1)为线性微分方程组。如果线性微分方程组中各未知函数的导数均为一阶的,则称为一阶线性微分方程组。其一般形式可写为
包含的各未知函数及其各阶导数都是一次的,则称方程组(1)为线性微分方程组。如果线性微分方程组中各未知函数的导数均为一阶的,则称为一阶线性微分方程组。其一般形式可写为
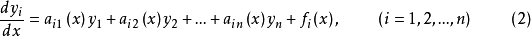 为简便计,(2)可写为向量形式
为简便计,(2)可写为向量形式
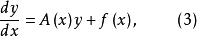 式中
式中
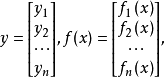
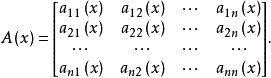 方程组(2)或(3)亦可称为n阶线性微分方程组(注意方程的阶与方程组的阶的定义),在(2)及(3)中,若
方程组(2)或(3)亦可称为n阶线性微分方程组(注意方程的阶与方程组的阶的定义),在(2)及(3)中,若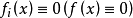 ,则称为齐次线性微分方程组;若相应的
,则称为齐次线性微分方程组;若相应的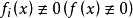 ,则称为非齐次线性微分方程组。2
,则称为非齐次线性微分方程组。2
注意点: 一般地,线性微分方程组均可化为一阶线性微分方程组的典则形式。2
一阶线性微分方程组因为常微分方程的所有数值算法都是以一阶微分方程组为求解对象的,而任何阶的常微分方程都可转化为一阶微分方程组的形式,故需要学习一阶微分方程组的解法。可使用求解代数方程组的高斯消元法求解一阶微分方程组。3
高斯消元法是求解线性方程组直接法中最常用和最有效的方法之一,其基本思想就是逐次消去一个未知数,使方程变换为一个等价方程组,然后求解该等价方程组,通过回代得到的解,再求解原方程的解。下面以例题介绍一阶线性微分方程组的解法。
例题1 解一阶微分方程组。
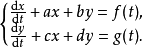 解:该一阶线性微分方程组含有自变量t,两个因变量
解:该一阶线性微分方程组含有自变量t,两个因变量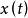 和
和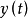 ,不能直接分离变量。故使用高斯消元法求解该方程组。从第一个方程解出y得
,不能直接分离变量。故使用高斯消元法求解该方程组。从第一个方程解出y得
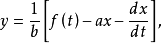 对t求导得
对t求导得
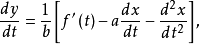 代入第二个式子得
代入第二个式子得
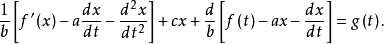 即消元得到不含因变量
即消元得到不含因变量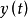 的二阶线性微分方程
的二阶线性微分方程
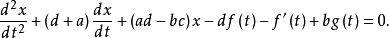 使用求解二阶线性微分方程的方法求解二阶线性微分方程,解出后代入式
使用求解二阶线性微分方程的方法求解二阶线性微分方程,解出后代入式 ,可解出y。3
,可解出y。3
高阶常系数线性微分方程组常系数线性微分方程组的求法:
(1)从方程组中消去一些未知函数及其各阶导数,得到只含有一个未知函数的高阶常系数线性微分方程。
(2)解此高阶微分方程,求出满足该方程的未知函数。
(3)把已求得的函数代入原方程组,一般来说。不必经过积分就可求出其余的未知函数。1
例题2 解方程组
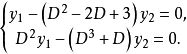
**解:**用消元法求解该方程组,消去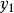 较为简便。用
较为简便。用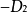 乘第一个式子与第二个式子相加,得
乘第一个式子与第二个式子相加,得
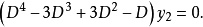 求解上式的特征方程
求解上式的特征方程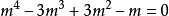 ,得到
,得到
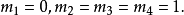 解得
解得
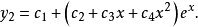 把上式代入第一个式子即求出
把上式代入第一个式子即求出
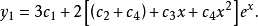




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国