[科普中国]-标准部分定理

标准部分定理断言：设x是任意一个有限超实数，则存在惟一的实数r，使得x与r无限接近，记为r=st(x)或r=°x，r称为x的标准部分。

简介标准部分定理是关于有限超实数与实数的关系的一个定理。

该定理断言：设x是任意一个有限超实数，则存在惟一的实数r，使得x与r无限接近，记为r=st(x)或r=°x，r称为x的标准部分。1

超实数(Hyperreal number)

超实数是一个包含实数以及无穷大和无穷小的域，它们的绝对值分别大于和小于任何正实数。

美国数理逻辑学家A.鲁宾逊于1960年创立。鲁宾逊证明，实数结构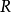可扩张为包含无穷小数和无穷大数的结构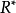，在一定意义下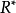与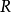有相同的性质。称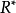中的数为超实数，形象地说，是在普通实数中又加进了无穷小数（其绝对值小于任何实数）及无穷大数（其绝对值大于任何实数）。

实数实数，是有理数和无理数的总称。数学上，实数定义为与数轴上的实数，是有理数和无理数的总称。数学上，实数定义为与数轴上的实数，点相对应的数。实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。

实数可以分为有理数和无理数两类，或代数数和超越数两类。实数集通常用黑正体字母R表示。R表示n维实数空间。实数是不可数的。实数是实数理论的核心研究对象。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所