[科普中国]-对称张量

定义

如果一个p次反变张量在自然同构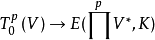下所对应p线性型是对称的，则称此张量为对称张量。

对于共变张量，如果它在自然同构下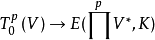所对应的p线性型是对称的，则称此张量为对称张量。

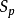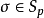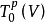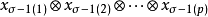也可以如下直接定义，为简单起见，假设域K的特征不为2，以表示p次对称群。对于任意的，上将对应于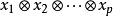的线性变换是唯一确定的，且是正则的，仍以σ表示。同样地，也可以唯一确定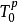的正则线性变换σ。张量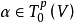是对称张量当且仅当对于任意，恒有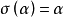。如果α的分量是，那么α是对称的充分必要条件是它的分量关于指标的置换是对称的。1

对称化子(p,0)型张量空间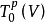或(0,p)型张量空间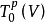的线性变换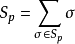称为对称化子，这里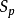表示p次对称群。任意张量α在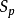下的像是对称张量。

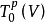的对称张量构成的子空间是关于张量表示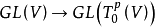的不变子空间。