[科普中国]-高阶微分方程

高阶微分方程是含有未知函数的导数高于一阶的微分方程。求解方程高阶微分方程的重要的方法就是降阶法。

定义阶数高于一的微分方程通称为高阶微分方程。1

形如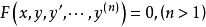 的方程称为高阶微分方程，式中F是所有变元的连续函数。

求解方法一般来说，高阶微分方程的求解比较复杂，在此仅介绍几种容易求解的类型，这几种方程的解法思路主要是利用变换将高阶方程化为较低阶的方程，将这种方法称为降阶法（method of reduction of order）。

一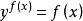型的微分方程

形如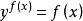的方程，这类方程只要逐次积分n次就可以得到其通解，每积分一次得到一个任意常数，在通解中含有n个任意常数。

二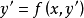型的微分方程

形如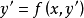型的方程，这类方程的特点是右端函数不显含未知函数y。

如果设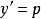，则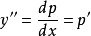，微分方程变为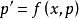，这是一个关于变量x，p的一阶微分方程。

设其通解为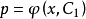，由于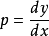，因此又得到一个一阶微分方程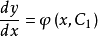，两边积分，便得到方程式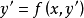的通解为。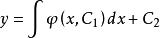

三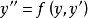型的微分方程

形如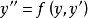型的方程，这类方程的特点是右端函数不显含自变量x。

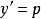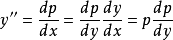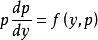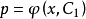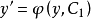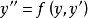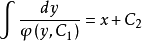设，这时可以将y看作新的自变量，p作为y的函数，则有，于是微分方程就变为，这是一个关于变量y，p的一阶微分方程，设它的通解为，即，将方程分离变量并积分，便得到的通解为。2

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学