[科普中国]-非齐次线性微分方程

一阶线性微分方程可分两类，一类是齐次形式的，它可以表示为y'+p(x)y=0，另一类就是非齐次形式的，它可以表示为y'+p(x)y=Q(x)。

齐次线性方程与非齐次方程比较一下对理解齐次与非齐次微分方程是有利的。对于非齐次微分方程的解来讲，类似于线性方程解的结构结论还是成立的。就是：非齐次微分方程的通解可以表示为齐次微分方程的通解加上一个非齐次方程的特解。

一阶非齐次线性微分方程的求解：

1 一阶非齐次线性微分方程y'+p(x)y=Q(x)，若设 ，则该方程的等价方程为 。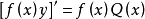

2若 是一阶齐次线性方程y'+p(x)y=0的通解，则一阶非齐次线性方程y'+p(x)y=Q(x)的通解

解满足。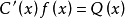

二阶非齐次线性微分方程的求解：

二阶常系数非齐次线性微分方程的表达式为y''+py'+qy=f(x)，它的特解

，

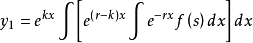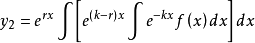
（1） 当时，r和k都是实数，y*=y1是方程的特解。

（2）当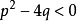时，r=a+ib,k=a-ib(b≠0)是一对共轭复根，y*=1/2（y1+y2）是方程的实函数解。

三阶非齐次线性微分方程的求解：

三阶常系数非齐次线性微分方程的表达式为y'''+p1y''+p2y'+p3y=f(x)，设其特征方程的三个特征跟分别是r1，r2，r3，特解为

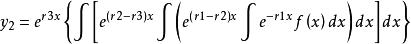
（1）当r1，r2，r3都是实数时，y*=y1是方程的特解。

（2）当r1是实数，r2，r3是共轭复数时，则y1和y2是共轭复数，因此，y*=1/2（y1+y2）是方程的实函数解2。

高阶非齐次线性微分方程的求解：

一般形式的n 阶非齐次线性微分方程

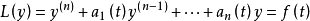
对应的齐次线性微分方程为

其中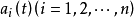及f(t)都是R上的连续函数。

如果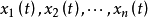是齐次方程的一个基本解组，而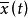是非齐次方程的某个解，则非齐次方程的通解可以表示为

其中c1,c2,...,cn是任意常数。

若n阶非齐次线性微分方程的柯西函数U(t,s)及U^(k)(t,s)(k=1,2,...,n)均连续，函数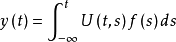及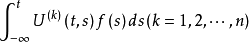都是一致收敛的，则函数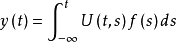是非齐次线性微分方程的一个解3。